【题目】在菱形ABCD中,点Q为AB边上一点,点F为BC边上一点连接DQ、DF和QF.
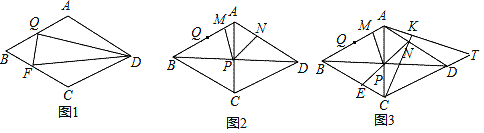
(1)如图1,若∠ADQ=∠FDQ,∠FQD=90°,求证:AQ=BQ;
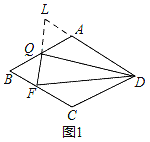
(2)如图2,在(1)的条件下,∠BAD=120°,对角线AC、BD相交于点P,以点P为顶点作∠MPN=60°,PM与AB交于点M,PN与AD交于点N,求证:DN+QM=AB;
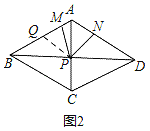
(3)如图3,在(1)(2)的条件下,延长NP交BC于点E,延长CN到点K,使CK=CA,连接AK并延长和CD的延长线交于点T,若AM:DN=1:5,S四边形MBEP=12![]() ,求线段DT的长.
,求线段DT的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)DT=4.
【解析】
(1)作辅助线,证明△FQD≌△LQD和△ALQ≌△BFQ,可得结论;
(2)如图2,连接QP,由AQ=BQ,并根据直角三角形斜边中线的性质得:PA=PQ,所以△APQ是等边三角形,证明△PQM≌△PAN(ASA),则QM=AN,根据AB=AD=DN+AN,代入可得结论;
(3)如图3,作辅助线,构建直角△AMG和直角△CEH,设AM=a,则DN=5a,根据(2):AB=DN+QM,得AB=8a,证明△PCE≌△PAN,得CE=AN=3a,根据勾股定理计算BP和MG、EH的长,根据S四边形MBEP=12![]() ,列方程可得a的值,
,列方程可得a的值,
则AM=1,AN=3,DN=5,CD=8,过C作CI⊥AD于I,得ID=![]() CD=
CD=![]() ×8=4,根据勾股定理得CN的长;
×8=4,根据勾股定理得CN的长;
在CD上截取CS,使CS=DN=5,连接AS,证明△ACS≌△CDN(SAS),可得结论.
证明:(1)如图1,分别延长FQ、DA交于L,
∵∠ADQ=∠FDQ,DQ=DQ,∠FQD=∠LQD=90°,
∴△FQD≌△LQD(ASA),
∴FQ=LQ,
∵四边形ABCD是菱形,
∴LD∥BF,
∴∠ALQ=∠BFQ,∠LAQ=∠FBQ,
∴△ALQ≌△BFQ,
∴AQ=BQ;
(2)如图2,连接QP,
∵四边形ABCD是菱形,
∴∠BAP=∠DAP,PA=PC,AC⊥BD,
∴∠APB=∠APD=90°,
∵∠BAD=120°,
∴∠BAP=∠DAP=60°,
∴∠ABP=30°,
∴PA=![]() AB,
AB,
∵AQ=BQ,
∴PQ=![]() AB,
AB,
∴PA=PQ,
∴△APQ是等边三角形,
∴∠APQ=∠PQA=60°,
∵∠MPN=60°,
∴∠APQ=∠MPN=60°,
∴∠QPM=∠APN,
∵∠PQM=∠PAN=60°,
∴△PQM≌△PAN(ASA),
∴QM=AN,
∵AB=AD=DN+AN,
∴AB=DN+QM;
(3)解:如图3,过点M作MG⊥AC于G,过点E作EH⊥AC于H,设AM=a,
∵AM:DN=1:5,
∴DN=5a,
由(2)知:AB=DN+QM,
∵AQ=![]() AB,QM=AQ﹣AM,
AB,QM=AQ﹣AM,
∴5a+![]() AB﹣a=AB,AB=8a,
AB﹣a=AB,AB=8a,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=8a,
∴AN=3a,
∵∠APN=∠CPE,AP=CP,∠DAC=∠BCA=60°,
∴△PCE≌△PAN(ASA),
∴CE=AN=3a,
Rt△BPC中,∠CBP=30°,BC=8a,
∴BP=4![]() a,
a,
同理MG=![]() a,EH=
a,EH=![]() a,
a,
∵S四边形MBEP=S△ABC﹣S△APM﹣S△CPE,
∴![]() ﹣
﹣![]() ﹣
﹣![]() =12
=12![]() ,
,
∴a2=1,a=1(a=﹣1舍去),
∴AM=1,AN=3,DN=5,CD=8,
过C作CI⊥AD于I,
∴ID=![]() =
=![]() ,
,
∴NI=ND﹣ID=5﹣4=1,
在Rt△CID中,CD2=DI2+CI2,
∴CI2=CD2﹣ID2=82﹣42=48,
在Rt△ICN中,CN2=NI2+CI2,
∴CN2=1+48=49,
∴CN=7,
在CD上截取CS,使CS=DN=5,连接AS,
∴AN=SD=3,
∵∠ACS=∠CDN=60°,AC=CD,
∴△ACS≌△CDN(SAS),
∴∠CAS=∠DCN,SA=NC=7,
∵CA=CK,
∴∠CAK=∠CKA,
∴∠SAK=∠KTC,
∴SA=ST=7,
∴DT=7﹣3=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张)
零售价(元/张)
成套售价(元/套)
餐桌
a
270
500元
餐椅
a﹣110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )

A.160
B.161
C.162
D.163 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个圆锥的侧面积是它底面积的2倍,则这个圆锥的侧面展开图的圆心角是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,点B和点C分别是x轴的正半轴和y轴的正半轴上的两点,且OB:BC=1:
 ,直线BC的解析式为y=﹣kx+6k(k≠0).
,直线BC的解析式为y=﹣kx+6k(k≠0).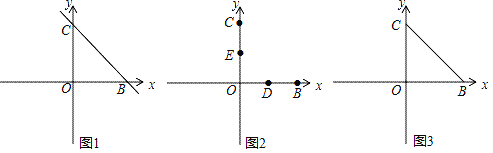
(1)如图1,求点C的坐标;
(2)如图2,点D为OB中点,点E为OC中点,点F在y轴的负半轴上,点A是射线FD上的第一象限的点,连接AE、ED,若FD=DA,且S△AED=
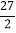 ,求点A的坐标;
,求点A的坐标;(3)如图3,在(2)的条件下,点P在线段OB上,点Q在线段OC的延长线上,CQ=BP,连接PQ与BC交于点M,连接AM并延长AM到点N,连接QN、AP、AB和NP,若∠QPA﹣∠NQO=∠NQP﹣∠PAB,NP=2
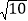 ,求直线PQ的解析式.
,求直线PQ的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A、B、C,完成下列问题:

(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E为BA的中点(E到A、C两点的距离相等),井在数轴上标出点E表示的数,求出CE的长.
(3)O为原点,取OC的中点M,分OC分为两段,记为第一次操作:取这两段OM、CM的中点分别为了N1、N2,将OC分为4段,记为第二次操作,再取这两段的中点将OC分为8段,记为第三次操作,第六次操作后,OC之间共有多少个点?求出这些点所表示的数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .

相关试题

