【题目】下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( ) 
A.160
B.161
C.162
D.163
参考答案:
【答案】B
【解析】方法一: 解:第一个图形正三角形的个数为5,
第二个图形正三角形的个数为5×3+2=17,
第三个图形正三角形的个数为17×3+2=53,
第四个图形正三角形的个数为53×3+2=161,
故选B.
方法二:![]() ,
, ![]() ,
, ![]() ,
, 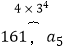 ,…
,… 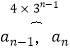 ,
,
∴  ,
,
(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(an﹣an﹣1)=an﹣a1 ,
∴an﹣a1=4×(3+32+…+3n﹣1)=4×(3+32+…+3n﹣1)= ![]() (用错位相减法可求出)
(用错位相减法可求出)
∴ ![]() ,
,
∵a1=5,
∴ ![]() .
.
由图可以看出:第一个图形中由角上的3个三角形加上中间1个小三角形再加上外围1个大三角形共有5个正三角形;下一个图形的三个角上的部分是上一个图形的全部,另外加上中间一个小的三角形和外围的一个大三角形,所以第二个图形中有5×3+1+1=17个正三角形,第三个图形中有17×3+1+1=53个正三角形,第四个图形中有53×3+1+1=161个正三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在四边形ABCD中,∠ABC=∠DCB=90°,点P在BC边上,连接AP和PD,点E在DC边上,连接BE与DP和AP分别交于点F和点G,若AB=PC,BP=DC,∠DFE=45°.
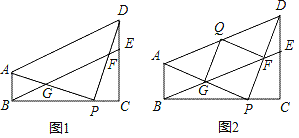
(1)如图1,求证:四边形ABED为平行四边形;
(2)如图2,把△PFG沿FG翻折,得到△QFG(点P与点Q为对应点),点Q在AD上,在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形(不包括平行四边形ABED,但包括特殊的平行四边形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3x+7=2x﹣5 ;
(2)2(x﹣1)﹣3(2+x)=5;
(3)
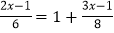
(4)
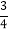 [
[ (
( ﹣
﹣ )]=
)]=  +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张)
零售价(元/张)
成套售价(元/套)
餐桌
a
270
500元
餐椅
a﹣110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个圆锥的侧面积是它底面积的2倍,则这个圆锥的侧面展开图的圆心角是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,点Q为AB边上一点,点F为BC边上一点连接DQ、DF和QF.
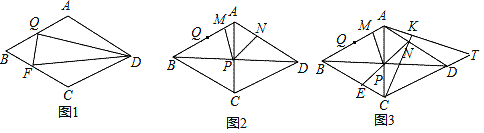
(1)如图1,若∠ADQ=∠FDQ,∠FQD=90°,求证:AQ=BQ;
(2)如图2,在(1)的条件下,∠BAD=120°,对角线AC、BD相交于点P,以点P为顶点作∠MPN=60°,PM与AB交于点M,PN与AD交于点N,求证:DN+QM=AB;
(3)如图3,在(1)(2)的条件下,延长NP交BC于点E,延长CN到点K,使CK=CA,连接AK并延长和CD的延长线交于点T,若AM:DN=1:5,S四边形MBEP=12
 ,求线段DT的长.
,求线段DT的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,点B和点C分别是x轴的正半轴和y轴的正半轴上的两点,且OB:BC=1:
 ,直线BC的解析式为y=﹣kx+6k(k≠0).
,直线BC的解析式为y=﹣kx+6k(k≠0).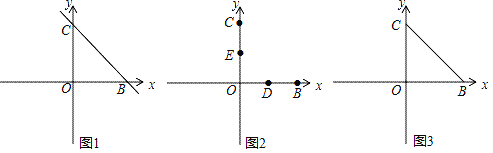
(1)如图1,求点C的坐标;
(2)如图2,点D为OB中点,点E为OC中点,点F在y轴的负半轴上,点A是射线FD上的第一象限的点,连接AE、ED,若FD=DA,且S△AED=
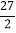 ,求点A的坐标;
,求点A的坐标;(3)如图3,在(2)的条件下,点P在线段OB上,点Q在线段OC的延长线上,CQ=BP,连接PQ与BC交于点M,连接AM并延长AM到点N,连接QN、AP、AB和NP,若∠QPA﹣∠NQO=∠NQP﹣∠PAB,NP=2
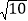 ,求直线PQ的解析式.
,求直线PQ的解析式.
相关试题

