【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 
参考答案:
【答案】2 ![]() ﹣2
﹣2
【解析】解:①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“,即当点P与点A重合时,PD值最小,为2; ②若以边PC为底,∠PBC为顶角时,以点B为圆心,BC长为半径作圆,与BD相交于一点,则弧AC(除点C外)上的所有点都满足△PBC是等腰三角形,当点P在BD上时,PD最小,最小值为2√3﹣2;
③若以边PB为底,∠PCB为顶角,以点C为圆心,BC为半径作圆,则弧BD上的点A与点D均满足△PBC为等腰三角形,当点P与点D重合时,PD最小,显然不满足题意,故此种情况不存在;
综上所述,PD的最小值为2 ![]() ﹣2.
﹣2.
分三种情形讨论①若以边BC为底.②若以边PC为底.③若以边PB为底.分别求出PD的最小值,即可判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,点Q为AB边上一点,点F为BC边上一点连接DQ、DF和QF.
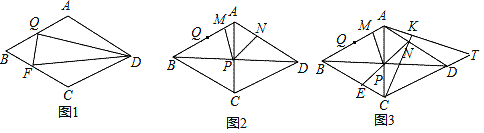
(1)如图1,若∠ADQ=∠FDQ,∠FQD=90°,求证:AQ=BQ;
(2)如图2,在(1)的条件下,∠BAD=120°,对角线AC、BD相交于点P,以点P为顶点作∠MPN=60°,PM与AB交于点M,PN与AD交于点N,求证:DN+QM=AB;
(3)如图3,在(1)(2)的条件下,延长NP交BC于点E,延长CN到点K,使CK=CA,连接AK并延长和CD的延长线交于点T,若AM:DN=1:5,S四边形MBEP=12
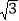 ,求线段DT的长.
,求线段DT的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,点B和点C分别是x轴的正半轴和y轴的正半轴上的两点,且OB:BC=1:
 ,直线BC的解析式为y=﹣kx+6k(k≠0).
,直线BC的解析式为y=﹣kx+6k(k≠0).
(1)如图1,求点C的坐标;
(2)如图2,点D为OB中点,点E为OC中点,点F在y轴的负半轴上,点A是射线FD上的第一象限的点,连接AE、ED,若FD=DA,且S△AED=
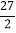 ,求点A的坐标;
,求点A的坐标;(3)如图3,在(2)的条件下,点P在线段OB上,点Q在线段OC的延长线上,CQ=BP,连接PQ与BC交于点M,连接AM并延长AM到点N,连接QN、AP、AB和NP,若∠QPA﹣∠NQO=∠NQP﹣∠PAB,NP=2
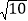 ,求直线PQ的解析式.
,求直线PQ的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A、B、C,完成下列问题:

(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E为BA的中点(E到A、C两点的距离相等),井在数轴上标出点E表示的数,求出CE的长.
(3)O为原点,取OC的中点M,分OC分为两段,记为第一次操作:取这两段OM、CM的中点分别为了N1、N2,将OC分为4段,记为第二次操作,再取这两段的中点将OC分为8段,记为第三次操作,第六次操作后,OC之间共有多少个点?求出这些点所表示的数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:|﹣ |+(
|+(  )﹣1﹣2cos45°.
)﹣1﹣2cos45°.
(2)解方程: +
+  =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( )
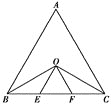
A. 6个 B. 5个 C. 4个 D. 3个
相关试题

