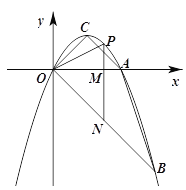
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为y=-x2+2x;C(1,1);(2)N1(1,-1),N2(2,-2),N3(![]() ,
, ![]() )P1(
)P1(![]() ,
, ![]() ),P2(
),P2(![]() ,
, ![]() );(3)
);(3)![]() 或
或![]()
【解析】(1)本题需先根据抛物线y=ax2+bx(a≠0)经过(2,0)B(3,-3)两点,分别求出a、b的值,再代入抛物线y=ax2+bx即可求出它的解析式;
(2)由△PON为等腰三角形的条件,依次写出点N、点P的坐标;
(3)作BD⊥x轴于D,作CE⊥x轴于E,交OB于F,由三角形面积求出OE=EF,然后分几种情况得到m 的值.
解:(1)根据题意,得![]() ,解这个方程组得
,解这个方程组得![]()
∴抛物线的解析式为y=-x2+2x
当x=![]() 时,y=-x2+2x=1,∴C(1,1)
时,y=-x2+2x=1,∴C(1,1)
(2)N1(1,-1),N2(2,-2),N3(![]() ,
, ![]() )
)
P1(![]() ,
, ![]() ),P2(
),P2(![]() ,
, ![]() )
)
(3)作BD⊥x轴于D,作CE⊥x轴于E,交OB于F
则BD=OD=3,CE=OE=1,OC=AC
∴△ODB,△OCE,△AOC均为等腰直角三角形
![]()
∴∠AOC=∠AOB=∠OAC=45°
∵PM∥y轴,∴OM⊥PN,∠MNO=∠AOB=45°,∴OM=MN=m,OE=EF=1
①∵![]()
∴当0<m≤1时,不能满足条件
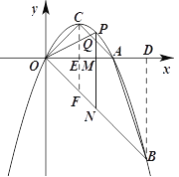
②当1<m≤2时,设PN交AC于Q,则MQ=MA=2-m
![]()
由![]() ,得
,得![]() ,解得
,解得![]()
![]() ,符合题意
,符合题意
由![]() ,得
,得![]() ,解得
,解得![]()
![]() ,符合题意
,符合题意
③当2<m<3时,作AG⊥x轴,交OB于G,
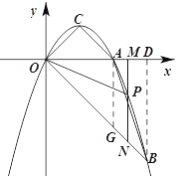
则AG=OA=2,AD=1
∴![]()
∴当2<m<3时,不能满足条件
∴![]() 或
或![]()
“点睛”此题属于二次函数综合题,涉及了待定系数法求函数解析式、一元一次方程的解及三角形的面积,综合性较强,解答本题的难点在第三问,关键是根据题意进行分类求解,难度较大,一般出是试题的压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各组数据中,不能作为直角三角形的三边边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
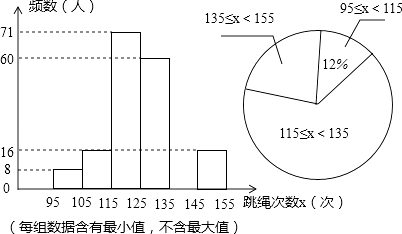
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x<155所在扇形的圆心角度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀?
(4)请你根据以上信息,对我市开展的学生跳绳活动谈谈自己的看法或建议. -
科目: 来源: 题型:
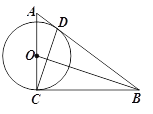
查看答案和解析>>【题目】如图,在△ABC中,∠ ACB=90°,点D在BC边上,且BD=BC,过点B作CD的垂线交AC于点O,以O为圆心,OC为半径画圆.
(1)求证:AB是⊙O的切线;
(2)若AB=10,AD=2,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD的对角线相交于点O,将线段OD绕点O旋转,使点D的对应点落在BC延长线上的点E处,OE交CD于H,连接DE.
(1)求证:DE⊥BC;
(2)若OE⊥CD,求证:2CE·OE=CD·DE;
(3)若OE⊥CD,BC=3,CE=1,求线段AC的长.

-
科目: 来源: 题型:
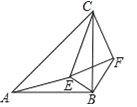
查看答案和解析>>【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF.
(2)若BE=1,AE=2,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别为5厘米、9厘米,则这个三角形的周长为________.
相关试题

