【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题: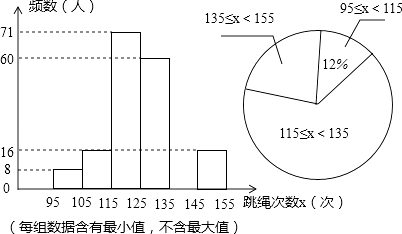
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x<155所在扇形的圆心角度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀?
(4)请你根据以上信息,对我市开展的学生跳绳活动谈谈自己的看法或建议.
参考答案:
【答案】
(1)解:抽查的总人数:(8+16)÷12%=200(人)
(2)解:范围是135≤x<145的人数是:200﹣8﹣16﹣71﹣60﹣16=29(人),
则跳绳次数范围135≤x<155所在扇形的圆心角度数是:360× ![]() =81°.
=81°.
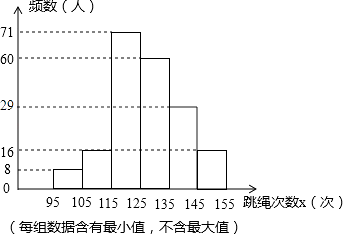
(3)解:优秀的比例是: ![]() ×100%=52.5%,
×100%=52.5%,
则估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是:8000×52.5%=4200(人)
(4)解:全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好
【解析】①根据统计图得到抽查的总人数:(8+16)÷12%=200(人);②根据范围是135≤x<145的人数是:200﹣8﹣16﹣71﹣60﹣16=29(人),则跳绳次数范围135≤x<155所在扇形的圆心角度数是81°;③根据优秀的比例是:(60+29+16)÷200=0.525=52.5%,则估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是:8000×52.5%=4200(人);④全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.
【考点精析】通过灵活运用频数分布直方图和扇形统计图,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况即可以解答此题.
-
科目: 来源: 题型:
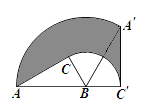
查看答案和解析>>【题目】如图,在△ABC中,AC=3cm,∠ACB=90°,∠ABC=60°,将△ABC绕点B顺时针旋转至△A′BC′,点C′在直线AB上,则边AC扫过区域(图中阴影部分)的面积为____________cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于整式(x﹣2)(x+n)运算结果中,一次项系数为2,则n=
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各组数据中,不能作为直角三角形的三边边长的是( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
-
科目: 来源: 题型:
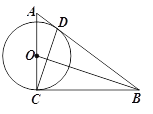
查看答案和解析>>【题目】如图,在△ABC中,∠ ACB=90°,点D在BC边上,且BD=BC,过点B作CD的垂线交AC于点O,以O为圆心,OC为半径画圆.
(1)求证:AB是⊙O的切线;
(2)若AB=10,AD=2,求⊙O的半径.
-
科目: 来源: 题型:
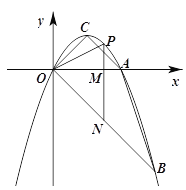
查看答案和解析>>【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD的对角线相交于点O,将线段OD绕点O旋转,使点D的对应点落在BC延长线上的点E处,OE交CD于H,连接DE.
(1)求证:DE⊥BC;
(2)若OE⊥CD,求证:2CE·OE=CD·DE;
(3)若OE⊥CD,BC=3,CE=1,求线段AC的长.

相关试题

