【题目】一个等腰三角形的两边长分别为5厘米、9厘米,则这个三角形的周长为________.
参考答案:
【答案】19厘米或23厘米
【解析】
运用分类讨论的思想和三角形三边关系的知识去解题.题中没有给出有腰长为5cm还是9cm,所以要分两种情况去讨论,特别要注意的是要判断三边是否能组成三角形.
解: 该三角形是等腰三角形,①当腰长为5厘米时,三边长为5厘米,5厘米,9厘米,此时5+5>9,则这三边能组成三角形,其周长为19厘米;②当腰长为9厘米时,三边长为5厘米,9厘米,9厘米,此时5+9>9,则这三边能组成三角形,其周长为23厘米.综上,答案为19厘米或23厘米.
-
科目: 来源: 题型:
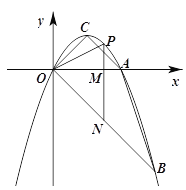
查看答案和解析>>【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD的对角线相交于点O,将线段OD绕点O旋转,使点D的对应点落在BC延长线上的点E处,OE交CD于H,连接DE.
(1)求证:DE⊥BC;
(2)若OE⊥CD,求证:2CE·OE=CD·DE;
(3)若OE⊥CD,BC=3,CE=1,求线段AC的长.

-
科目: 来源: 题型:
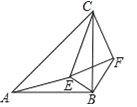
查看答案和解析>>【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF.
(2)若BE=1,AE=2,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y﹦(m+1)x+m2﹣1是正比例函数,则m的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2x+1)(x﹣1)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把弯曲的河道改成直的,可以缩短航程,其理由是( )
A. 经过两点有且只有一条直线
B. 两点之间,线段最短
C. 两点之间,直线最短
D. 线段可以比较大小
相关试题

