【题目】根据2019年莆田市初中毕业升学体育考试内容要求,甲、乙、丙在某节体育课他们各自随机分别到篮球场A处进行篮球运球绕杆往返训练或到足球场B处进行足球运球绕杆训练,三名学生随机选择其中的一场地进行训练.
(1)用列表法或树形图表示出的所用可能出现的结果;
(2)求甲、乙、丙三名学生在同一场地进行训练的概率;
(3)求甲、乙、丙三名学生中至少有两人在B处场地进行训练的概率.
参考答案:
【答案】(1)共有8种可能;(2)![]() ;(3)
;(3)![]()
【解析】
(1)用树状图分3次实验列举出所有情况即可;
(2)看3人在同一场地进行训练的情况数占总情况数的多少即可;
(3)看至少有两人在处场地进行训练的情况数占总情况数的多少即可.
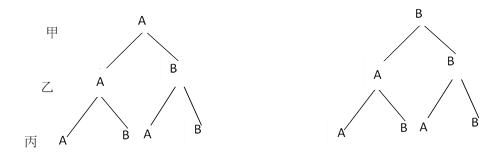
(1) 由上树状图可知甲、乙、丙三名学生进行体育训练共有8种可能,
(2)所有出现情况等可能,其中甲、乙、丙三名学生在同一场地进行训练有2种可能并把它记为事件A,则P(A)=![]()
(3) 其中甲、乙、1丙三名学生中至少有两人在B处场地进行训练有4种可能并把它记为事件B,则P(B)= ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
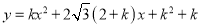 经过坐标原点.
经过坐标原点.(1)求抛物线的解析式和顶点B的坐标;
(2)设点A是抛物线与x轴的另一个交点且A、C两点关于y轴对称,试在y轴上确定一点P,使PA+PB最短,并求出点P的坐标;
(3)过点A作AD∥BP交y轴于点D,求到直线AP、AD、CP距离相等的点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=50米,若灰太狼以5米/秒的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克)
…
34.8
32
29.6
28
…
售价x(元/千克)
…
22.6
24
25.2
26
…
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
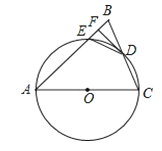
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
相关试题

