【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.

(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
参考答案:
【答案】(1)y=![]() x+1. (2)点C为线段AP的中点. (3)存在点D,使四边形BCPD为菱形,点D(8,1)即为所求.
x+1. (2)点C为线段AP的中点. (3)存在点D,使四边形BCPD为菱形,点D(8,1)即为所求.
【解析】试题分析:(1)由点A与点B关于y轴对称,可得AO=BO,再由A的坐标求得B点的坐标,从而求得点P的坐标,将P坐标代入反比例解析式求出m的值,即可确定出反比例解析式,将A与P坐标代入一次函数解析式求出k与b的值,确定出一次函数解析式;(2)由AO=BO,PB∥CO,即可证得结论 ;(3)假设存在这样的D点,使四边形BCPD为菱形,过点C作CD平行于x轴,交PB于点E,交反比例函数y=![]() 的图象于点D,分别连结PD、BD,如图所示,即可得点D(8,1), BP⊥CD,易证PB与CD互相垂直平分,即可得四边形BCPD为菱形,从而得点D的坐标.
的图象于点D,分别连结PD、BD,如图所示,即可得点D(8,1), BP⊥CD,易证PB与CD互相垂直平分,即可得四边形BCPD为菱形,从而得点D的坐标.
试题解析:
(1)∵点A与点B关于y轴对称,
∴AO=BO,
∵A(-4,0),
∴B(4,0),
∴P(4,2),
把P(4,2)代入y=![]() 得m=8,
得m=8,
∴反比例函数的解析式:y=![]()
把A(-4,0),P(4,2)代入y=kx+b
得: ![]() ,解得:
,解得: ![]() ,
,
所以一次函数的解析式:y=![]() x+1.
x+1.
(2)∵点A与点B关于y轴对称,
∴OA=OB
∵PB丄x轴于点B,
∴∠PBA=90°,
∵∠COA=90°,
∴PB∥CO,
∴点C为线段AP的中点.
(3)存在点D,使四边形BCPD为菱形
∵点C为线段AP的中点,
∴BC= ![]() ,
,
∴BC和PC是菱形的两条边
由y=![]() x+1,可得点C(0,1),
x+1,可得点C(0,1),
过点C作CD平行于x轴,交PB于点E,交反比例函数y=![]() 的图象于点D,
的图象于点D,
分别连结PD、BD,
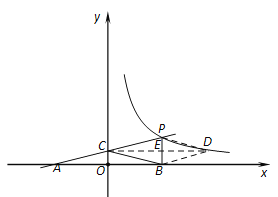
∴点D(8,1), BP⊥CD
∴PE=BE=1,
∴CE=DE=4,
∴PB与CD互相垂直平分,
∴四边形BCPD为菱形.
∴点D(8,1)即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富校园文化生活,某校计划在早间校园广播台播放“百家讲坛”的部分内容,为了了解学生的喜好,随机抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:
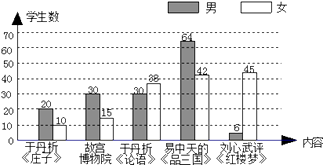
请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为名;
(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的%. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.已知四边形ABCD的中点四边形是正方形,对角线AC与BD的关系,下列说法正确的是( )
A. AC,BD相等且互相平分B. AC,BD垂直且互相平分
C. AC,BD相等且互相垂直D. AC,BD垂直且平分对角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.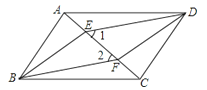
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师、杨老师两家所在位置关于学校成中心对称.如果王老师家距学校2千米,那么她们两家相距千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对同一平面内的三条直线a,b,c,给出下列5个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c.以其中两个论断为已知条件,另一个论断为结论,组成一个你认为正确的命题:______________(只填序号即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个多边形的边数之比为1∶2,两个多边形所有内角的和为1980°,求这两个多边形的边数.
相关试题

