【题目】已知:抛物线![]() 经过坐标原点.
经过坐标原点.
(1)求抛物线的解析式和顶点B的坐标;
(2)设点A是抛物线与x轴的另一个交点且A、C两点关于y轴对称,试在y轴上确定一点P,使PA+PB最短,并求出点P的坐标;
(3)过点A作AD∥BP交y轴于点D,求到直线AP、AD、CP距离相等的点的坐标.
参考答案:
【答案】(1)抛物线的解析式是y=﹣x2+2![]() x,顶点B的坐标是(
x,顶点B的坐标是(![]() ,3);(2)点P的坐标是(0,2);(3)到直线AP、AD、CP距离相等的点的坐标是(0,0)和(2
,3);(2)点P的坐标是(0,2);(3)到直线AP、AD、CP距离相等的点的坐标是(0,0)和(2![]() ,2).
,2).
【解析】
(1)根据抛物线经过原点求出k的值,即可求出解析式,在求顶点坐标即可;
(2)先找出P的位置,再求直线BC的解析式,再求点P的坐标即可;
(3)先求得y轴是∠APC的角平分线,x轴是∠DAP的角平分线,交点符合要求,∠DAP的外角∠EAP的平分线和∠CPA的外角∠FPA的平分线的交点M也符合要求.
解:(1)∵抛物线![]() 经过坐标原点,
经过坐标原点,
∴k2+k=0,
解得:k=0(舍去),k=﹣1,
∴抛物线的解析式是y=﹣x2+2![]() x,
x,
∴y=﹣x2+2![]() x,
x,
=﹣(x﹣![]() )2+3,
)2+3,
∴顶点B的坐标是(![]() ,3),
,3),
答:抛物线的解析式是y=﹣x2+2![]() x,顶点B的坐标是(
x,顶点B的坐标是(![]() ,3);
,3);
(2)当y=0时﹣x2+2![]() x=0,
x=0,
解得:x1=0,x2=2![]() ,
,
∴A的坐标是(2![]() ,0),
,0),
A关于y轴的对称点C的坐标是C(﹣2![]() ,0),
,0),
设直线BC的解析式是y=kx+b,
把B(![]() ,3),C(﹣2
,3),C(﹣2![]() ,0)代入得:
,0)代入得: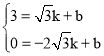 ,
,
解得: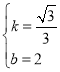 ,
,
∴直线BC的解析式是y=![]() x+2,
x+2,
当x=0时,y=2,
∴点P的坐标是(0,2),
答:点P的坐标是(0,2).
(3)∵A、C关于y轴对称,P在Y轴上,
∴AP=CP,
∵∠CAP=∠ACP,x轴⊥y轴,
∴y轴是∠APC的角平分线,
即y轴上任意一点到AP、CP的距离都相等,
∵AD∥PC,
∴∠DAC=∠ACP,
∴∠DAC=∠CAP,
∴x轴是∠DAP的角平分线,
即x轴上任意一点到AP、AD的距离都相等,
∴x轴与y轴的交点O到AP、AD、CP距离相等,
∴点的坐标是(0,0),
如图,
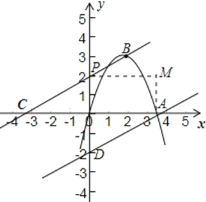
∠DAP的外角∠EAP的平分线和∠CPA的外角∠FPA的平分线的交点M也符合要求,
根据作图条件能得到矩形MAOP,
即点M的坐标是(2![]() ,2),
,2),
到直线AP、AD、CP距离相等的点的坐标是(0,0)和(2![]() ,2),
,2),
答:到直线AP、AD、CP距离相等的点的坐标是(0,0)和(2![]() ,2).
,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度
百分比
A非常了解
10%
B比较了解
15%
C基本了解
35%
D不了解
n%
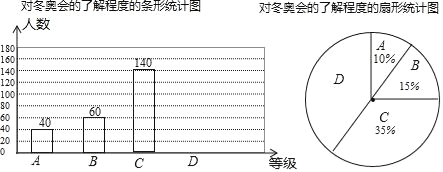
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
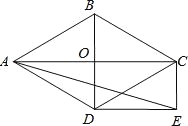
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2
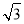 时,求sin∠AED的值,求∠EAD的正切值.
时,求sin∠AED的值,求∠EAD的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若
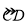 的长为
的长为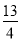 π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13
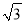 ,直接写出AP的长.
,直接写出AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=50米,若灰太狼以5米/秒的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据2019年莆田市初中毕业升学体育考试内容要求,甲、乙、丙在某节体育课他们各自随机分别到篮球场A处进行篮球运球绕杆往返训练或到足球场B处进行足球运球绕杆训练,三名学生随机选择其中的一场地进行训练.
(1)用列表法或树形图表示出的所用可能出现的结果;
(2)求甲、乙、丙三名学生在同一场地进行训练的概率;
(3)求甲、乙、丙三名学生中至少有两人在B处场地进行训练的概率.
相关试题

