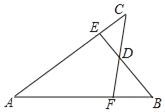
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
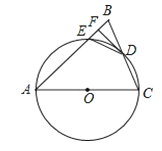
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
参考答案:
【答案】(1)见解析;(2)9.
【解析】试题分析: ![]() 首先连接OD,根据等腰三角形的性质可证∠C=∠ODC,从而可证∠B=∠ODC,根据DF⊥AB可证DF⊥OD,所以可证线DF与⊙O相切;
首先连接OD,根据等腰三角形的性质可证∠C=∠ODC,从而可证∠B=∠ODC,根据DF⊥AB可证DF⊥OD,所以可证线DF与⊙O相切;
![]() 根据圆内接四边形的性质可得:△BCA∽△BED,所以可证:
根据圆内接四边形的性质可得:△BCA∽△BED,所以可证: ![]() ,解方程求出BE的长度,从而求出AC的长度.
,解方程求出BE的长度,从而求出AC的长度.
试题解析: ![]() 如图所示,
如图所示,
连接![]() ,
,
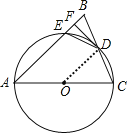
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∥
∥![]() ,
,
∵![]() ,
,
∴![]() ;
;
∵点![]() 在⊙O上,
在⊙O上,
∴直线![]() 与⊙O相切;
与⊙O相切;
![]() ∵四边形
∵四边形![]() 是⊙O的内接四边形,
是⊙O的内接四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴△BED∽△BCA,
∴![]() ,
,
∵OD∥AB, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
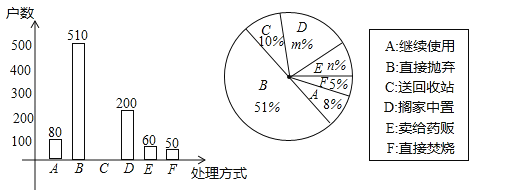
①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
-
科目: 来源: 题型:
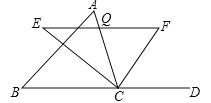
查看答案和解析>>【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
-
科目: 来源: 题型:
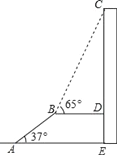
查看答案和解析>>【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈
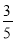 ,tan37°≈
,tan37°≈ ,sin65°≈
,sin65°≈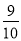 ,tan65°≈
,tan65°≈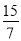 )
)
-
科目: 来源: 题型:
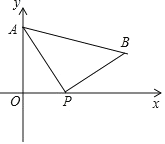
查看答案和解析>>【题目】如图,A(0,4)是直角坐标系 y 轴上一点,动点 P 从原点 O 出发,沿 x 轴正半轴运动,速度为每秒 1 个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为 t 秒.
(1)若 AB∥x 轴,求 t 的值;
(2)若OP=
 OA,求B点的坐标.
OA,求B点的坐标. (3)当 t=3 时,x 轴上是否存在有一点 M,使得以 M、P、A 为顶点的三角形是等腰三角形,请直接写出点 M 的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果一个点的纵坐标等于横坐标的2倍,那么这个点叫做倍点.例如:点(1,2)是倍点。
(1)已知第一象限内的点A到x轴的距离是1,若点A是倍点,则点A的坐标为________
(2)求反比例函数
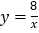 图像上的所有倍点;
图像上的所有倍点;(3)请分析一次函数
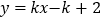 (
(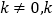 为常数)图像上倍点的情况.
为常数)图像上倍点的情况. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
A. ① B. ② C. ①和② D. ①②③
相关试题

