搜索
【题目】如图，等腰三角形
的底边
长为6，面积是36，腰
的垂直平分线
分别交，
边于
，
点，若点
为边的中点，点
为线段上一动点，则
周长的最小值____．
参考答案：
【答案】15
【解析】
连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AD的长为CM+MD的最小值，由此即可得出结论．
解：连接AD，
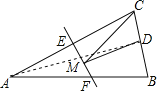
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC=
BCAD=×6×AD=36，解得AD=12，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短=（CM+MD）+CD=AD+BC=12+×6=12+3=15．
故答案为：15．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，抛物线与x轴交点坐标为A（1，0），C（-3，0），
（1）若已知顶点坐标D为（-1，4）或B点（0，3），选择适当方式求抛物线的解析式.
（2）若直线DH为抛物线的对称轴，在（1）的基础上，求线段DK的长度，并求△DBC的面积．
（3）将图（2）中的对称轴向左移动，交x轴于点p（m，0）(－3<m<－1)，与线段BC、抛物线的交点分别为点K、Q，用含m的代数式表示QK的长度，并求出当m为何值时，△BCQ的面积最大？
-
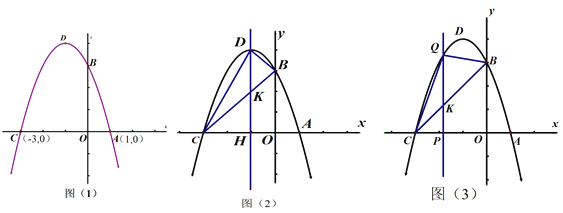
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线
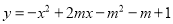交 y轴于点为A，顶点为D，对称轴与x轴交于点H．（1）求顶点D的坐标（用含m的代数式表示）；
（2）当抛物线过点（1，-2），且不经过第一象限时，平移此抛物线到抛物线
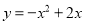的位置，求平移的方向和距离；（3）当抛物线顶点D在第二象限时，如果∠ADH=∠AHO，求m的值．
-
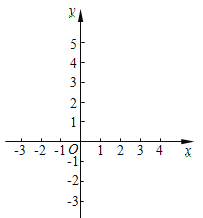
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
的三边
的长分别为
，其三条角平分线交于点
，则
=______．
-
科目： 来源： 题型：
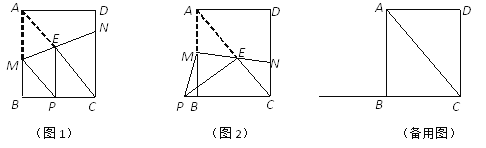
查看答案和解析>>【题目】已知：矩形ABCD中，AB＝4，BC＝3，点M、N分别在边AB、CD上，直线MN交矩形对角线 AC于点E，将△AME沿直线MN翻折，点A落在点P处，且点P在射线CB上.
(1)如图1，当EP⊥BC时，求CN的长；
(2) 如图2，当EP⊥AC时，求AM的长；
(3) 请写出线段CP的长的取值范围，及当CP的长最大时MN的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.
（1）求证：OE是CD的垂直平分线.
（2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下面的内容，再解决问题：
例题：若
+
+
-
+
=
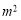，求
和
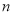的值．解：
++-+=
++
+-+=
（
）
+（-
）=
-=
-，
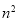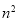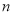问题：（1）若
-
-
=， 求
的值；（2）已知
的三边长
都是正整数，且满足
-
-
+
│3-
│=，请问是怎样形状的三角形．
相关试题
