搜索
【题目】试给出一组a，b的值，使得关于x的一元二次方程ax2+bx+1＝0有两个相等的实数根，并求出此时方程的根．
参考答案：
【答案】b＝2，a＝1，x1＝x2＝﹣1．
【解析】
由根的判别式△=b2-4a=0，可得出：若b=2，a=1，则原方程为x2+2x+1=0，解之即可得出结论．
解：方程ax2+bx+1＝0有两个相等的实数根，
∴△＝b2﹣4a＝0．
若b＝2，a＝1，则原方程为x2+2x+1＝0，即（x+1）2＝0，
解得：x1＝x2＝﹣1．
-
科目： 来源： 题型：
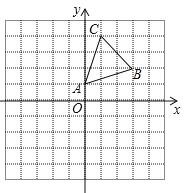
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．
（1）画出△ABC关于x轴的对称图形△A1B1C1；
（2）将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2，写出顶点A2，B2，C2的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】化简：
（1）
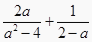
（2）
-
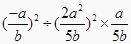
科目： 来源： 题型：
查看答案和解析>>【题目】请阅读下列材料：
∵
； 
； 
；
…
∴
=
=
=
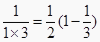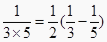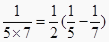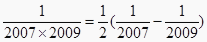
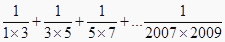
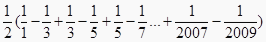
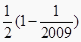
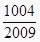
解答下列问题：
（1）在和式
中，第5项为 ， 第n项为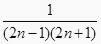 
，上述求和的想法是：将和式中的各分数转化为两个数之差，使得首末两项外的中间各项可以 ， 从而达到求和目的．
（2）利用上述结论计算：
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列比较大小正确的是（ ）
A.﹣（﹣3）＜+（﹣3）
B.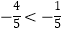
C.﹣|﹣12|＞11
D.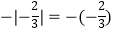
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t>0）秒。
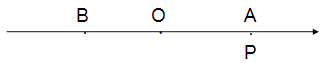
（1）写出数轴上点B表示的数 ， 点P表示的数（用含t的代数式表示）；
（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？
（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；
（4）若点D是数轴上一点，点D表示的数是x，请你探索式子|x+6|+|x-8|是否有最小值？如果有，直接写出最小值；如果没有，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算与解分式方程．
（1）
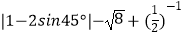
（2）
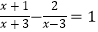
相关试题
