搜索
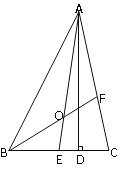
【题目】如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°，求∠DAC及∠BOA的度数.
参考答案：
【答案】∠DAC=20°，∠BOA=125°．
【解析】试题分析：根据AD⊥BC，则∠ADC=90°，根据△ADC的内角和可以求出∠DAC的度数，根据△ABC的内角和求出∠ABC的度数，然后根据角平分线的性质求出∠ABO+∠BAO的度数，最后根据△ABO的内角和求出∠BOA的度数．
试题解析：∵AD是高 ∴∠ADC=90° ∵∠C=70°∴∠DAC=180°﹣90°﹣70°=20°
∵∠BAC=50°，∠C=70°，AE是角平分线 ∴∠BAO=25°，∠ABC=60°
∵BF是∠ABC的角平分线 ∴∠ABO=30° ∴∠BOA=180°﹣∠BAO﹣∠ABO=125°
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题满分8分）如图，正方形网格中的每个小正方形边长都是1．
（利用网格线进行画图，别忘了标上字母噢！）
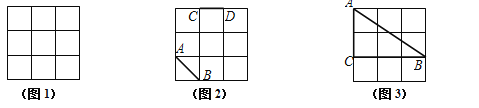
（1） 在图1中，画一个顶点为格点、面积为5的正方形；
（2） 在图2中，已知线段AB、CD，画线段EF，使它与AB、CD组成轴对称图形；
（要求画出所有符合题意的线段）
（3） 在图3中，找一格点D，满足：①到CB、CA的距离相等；②到点A、C的距离相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】深圳市教育局在全市中小学开展“四点半活动”试点工作.某校为了了解学生参与“四点半活动”项目的情况,对初中的部分学生进行了随机调查,调查项目分为“科技创新”类、“体育活动”类、“艺术表演”类、“植物种植”类及“其它”类共五大类别,并根据调查的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息，解答下面的问题
（1）请求出此次被调查学生的总人数人.
（2）根据以上信息,补全频数分布直方图.
（3）求出扇形统计图中,“体育活动”α的圆心角等于度.
（4）如果本校初中部有1800名学生,请估计参与“艺术表演”类项目的学生大约多
少人? -
科目： 来源： 题型：
查看答案和解析>>【题目】小明在求一个多边形的内角和时，由于疏忽，把一个内角加了两遍，而求出的结果为2004°，请问这个内角是多少度？这个多边形是几边形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程．
（1）在方程①3x－1=0，②
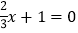③x－(3x+1)=－5 中，不等组
的关联方程是________ （2）若不等式组
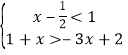的一个关联方程的根是整数， 则这个关联方程可以是________（写出一个即可） （3）若方程 3－x=2x，3+x=
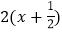都是关于 x 的不等式组 
的关联方程，直接写出 m 的取值范围. -
科目： 来源： 题型：
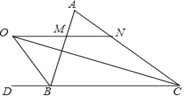
查看答案和解析>>【题目】如图，已知在△ABC中，△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O，MN过点O，且MN∥BC，分别交AB、AC于点M、N．
求证：（1）MO=MB；（2）MN=CN﹣BM．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，BD，CE分别是∠ABC，∠ACB平分线，BD，CE相交于点P．
（1）如图1，如果∠A=60°，∠ACB=90°，则∠BPC= ；
（2）如图2，如果∠A=60°，∠ACB不是直角，请问在（1）中所得的结论是否仍然成立？若成立，请证明：若不成立，请说明理由．
（3）小月同学在完成（2）之后，发现CD、BE、BC三者之间存在着一定的数量关系，于是她在边CB上截取了CF=CD，连接PF，可证△CDP≌△CFP，请你写出小月同学发现，并完成她的说理过程．
相关试题
