【题目】在△ABC中,BD,CE分别是∠ABC,∠ACB平分线,BD,CE相交于点P.
(1)如图1,如果∠A=60°,∠ACB=90°,则∠BPC= ;
(2)如图2,如果∠A=60°,∠ACB不是直角,请问在(1)中所得的结论是否仍然成立?若成立,请证明:若不成立,请说明理由.
(3)小月同学在完成(2)之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了CF=CD,连接PF,可证△CDP≌△CFP,请你写出小月同学发现,并完成她的说理过程.

参考答案:
【答案】(1) 120°; (2) 成立 (3) BC=CD+BE
【解析】
(1)先根据三角形内角和定理求出∠ABC=30,再用角平分线的意义求出∠PCB=45°,∠PBC=15°,最后用三角形的内角和定理即可得出结论;
(2)先根据角平分线的意义,求出∠ACB=2∠PCB,∠ABC=2∠PBC,再根据三角形的内角和定理求出∠ABC+∠ACB=120°,最后用三角形内角和定理即可得出结论;
(3)先判断出△DCP≌△FCP(SAS),得出CD=CF,∠DPC=∠FPC=60°,进而判断出∠PBF=∠PBE,即可判断出△FPB≌△EPB,最后用等量代换即可得出结论.
解:(1)∵∠A=60°,∠ACB=90°,根据三角形内角和定理得,∠ABC=180°﹣60°﹣90°=30°,
∵BD,CE分别是∠ABC,∠ACB平分线,
∴∠PCB=![]() ∠ACB=45°,∠PBC=
∠ACB=45°,∠PBC=![]() ∠PBC=15°,
∠PBC=15°,
在△PBC中,根据三角形的内角和定理得,∠BPC=180°﹣∠PCB﹣∠PBC=180°﹣45°﹣15°=120°,
(2)结论仍然成立,
理由:∵BD,CE分别是∠ABC,∠ACB平分线,
∴∠ACB=2∠PCB,∠ABC=2∠PBC,
∵∠A=60°,
在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∴2∠PCB+2∠PBC=120°,
∴∠PCB+∠PBC=60°,
在△PBC中,∠BPC+∠PCB+∠PBC=180°,
∴∠BPC=180°﹣(∠PCB+∠PBC)=180°﹣60°=120°
(3)BC=CD+BE,理由:如图2,

由(2)知,∠BPC=120°,
∴∠DPC=∠EPB=60°,在边CB上截取了CF=CD,连接PF,
∵CE是∠ACB的平分线,
∴∠DCP=∠FCP,
在△DCP和△FCP中,
 ,
,
∴△DCP≌△FCP(SAS),
∴CD=CF,∠DPC=∠FPC=60°,
∴∠BPC=∠BPC﹣∠FPC=60°=∠EPB,
∵BD是∠ABC的平分线,
∴∠PBF=∠PBE,
在△FPB和△EPB中,
 ,
,
∴△FPB≌△EPB,BF=BE,
∴BC=CF+BF=CD+BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=∠DCB,添加一个条件,使△ABC≌△DCB,你添加的条件是_____.(注:只需写出一个条件即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料后解决问题:
计算:(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据以上解决问题的方法,试着解决:
(3+1)(32+1)(34+1)(38+1)…(364+1)=__
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为________

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=
 (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在一条不完整的数轴上一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.

(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)如果点A、C表示的数互为相反数,求点B表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y=
 x﹣2
x﹣2 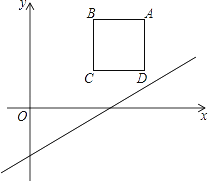
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
相关试题

