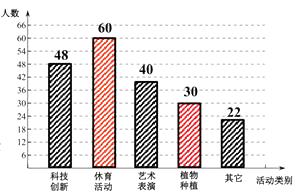
【题目】深圳市教育局在全市中小学开展“四点半活动”试点工作.某校为了了解学生参与“四点半活动”项目的情况,对初中的部分学生进行了随机调查,调查项目分为“科技创新”类、“体育活动”类、“艺术表演”类、“植物种植”类及“其它”类共五大类别,并根据调查的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题

(1)请求出此次被调查学生的总人数人.
(2)根据以上信息,补全频数分布直方图.
(3)求出扇形统计图中,“体育活动”α的圆心角等于度.
(4)如果本校初中部有1800名学生,请估计参与“艺术表演”类项目的学生大约多
少人?
参考答案:
【答案】
(1)200
(2)
解:“植物种植”类的人数:200×15%=30(人);
则“体育活动”类的人数:200-48-40-30-22=60(人). 补全频数分布直方图如下.
(3)108
(4)
解:1800× ![]() ×100%=360(人).
×100%=360(人).
答:参与“艺术表演”类项目的学生大约360人。
【解析】解: (1)“其它”类占11%,有22人,
则此次调查学生的总人数是22÷11%=200(人).
所以答案是200人.
3)由(2)可得“体育活动”类的人数是60人,则圆心角为360°× ![]() =108°;
=108°;
所以答案是108.
【考点精析】通过灵活运用扇形统计图和条形统计图,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强市民的节能意识,我市试行阶梯电价.从2013年开始,按照每户每年的分三个档次计费,具体规定见下图.小明统计了自己2013年前5个月的实际用电量为1300度,请帮助小明分析下面问题.

(1)若小明家计划2013年全年的用电量不超过2520度,则6至12月份小明家平均每月用电量最多为多少度?(保留整数)
(2)若小明家2013年6月至12月份平均每月用电量等于前5个月的平均每月用电量,则小明家2013年应交总电费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:

①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.
其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)如图,正方形网格中的每个小正方形边长都是1.
(利用网格线进行画图,别忘了标上字母噢!)
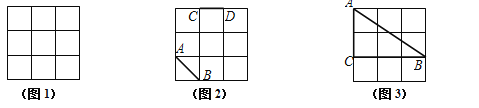
(1) 在图1中,画一个顶点为格点、面积为5的正方形;
(2) 在图2中,已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;
(要求画出所有符合题意的线段)
(3) 在图3中,找一格点D,满足:①到CB、CA的距离相等;②到点A、C的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在求一个多边形的内角和时,由于疏忽,把一个内角加了两遍,而求出的结果为2004°,请问这个内角是多少度?这个多边形是几边形?
-
科目: 来源: 题型:
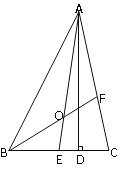
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC及∠BOA的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,②
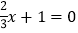 ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组 的关联方程是________
的关联方程是________ (2)若不等式组
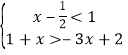 的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可) (3)若方程 3-x=2x,3+x=
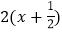 都是关于 x 的不等式组
都是关于 x 的不等式组  的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围.
相关试题

