搜索
【题目】小明在求一个多边形的内角和时，由于疏忽，把一个内角加了两遍，而求出的结果为2004°，请问这个内角是多少度？这个多边形是几边形？
参考答案：
【答案】24度，十三边形．
【解析】
n边形的内角和是（n-2）180°，因而内角和一定是180度的倍数．而多边形的内角一定大于0，并且小于180度，因而内角和再加上一个内角的值，所得结果除以180度，所得数值比边数n-2要大，且小于n-1，则用2004°除以180所得值的整数部分，加上2就是多边形的边数．
设这个多边形的边数为x，
依题意有（x﹣2）180=2004，
解得x=13
，
因而多边形的边数是13，该多边形为十三边形，
内角和是（13﹣2）×180°=1980°，因而这个内角是2004﹣1980=24°，
答：这个内角是24度，这个多边形是十三边形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：二次函数y=2x2+4x+m﹣1，与x轴的公共点为A，B．
（1）如果A与B重合，求m的值；
（2）横、纵坐标都是整数的点叫做整点； ①当m=1时，求线段AB上整点的个数；
②若设抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）整点的个数为n，当1＜n＜8时，结合函数的图象，求m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=BC，∠ABC=90°．以AB为斜边作等腰直角三角形ADB．点P是直线DB上一个动点，连接AP，作PE⊥AP交BC所在的直线于点E．
（1）如图1，点P在BD的延长线上，PE⊥EC，AD=1，直接写出PE的长；
（2）点P在线段BD上（不与B，D重合），依题意，将图2补全，求证：PA=PE；
（3）点P在DB的延长线上，依题意，将图3补全，并判断PA=PE是否仍然成立． -
科目： 来源： 题型：
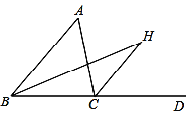
查看答案和解析>>【题目】如图，在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC的平分线，∠A =58°，求∠H的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们规定：平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d，点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D，定义点A到图形G的距离跨度为R=D﹣d．
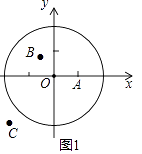
（1）①如图1，在平面直角坐标系xOy中，图形G1为以O为圆心，2为半径的圆，直接写出以下各点到图形G1的距离跨度： A（1，0）的距离跨度；
B（﹣
， 
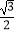）的距离跨度；
C（﹣3，﹣2）的距离跨度；
②根据①中的结果，猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是 ．
（2）如图2，在平面直角坐标系xOy中，图形G2为以D（﹣1，0）为圆心，2为半径的圆，直线y=k（x﹣1）上存在到G2的距离跨度为2的点，求k的取值范围．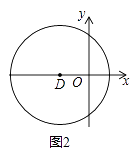
（3）如图3，在平面直角坐标系xOy中，射线OP：y=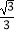
x（x≥0），⊙E是以3为半径的圆，且圆心E在x轴上运动，若射线OP上存在点到⊙E的距离跨度为2，直接写出圆心E的横坐标xE的取值范围 ．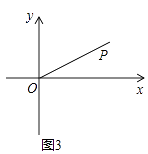 
-
科目： 来源： 题型：
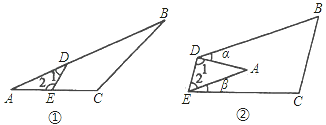
查看答案和解析>>【题目】（1）如图①所示，∠1+∠2与∠B+∠C有什么关系？为什么？
（2）如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时，则∠A与∠α+∠β之间有一种数量关系始终保持不变，请写出这个规律并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，BD⊥AC于D．若∠A：∠ABC：∠ACB=3：4：5，E为线段BD上任一点．
（1）试求∠ABD的度数；
（2）求证：∠BEC＞∠A．
相关试题
