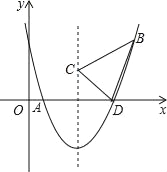
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2﹣4x+6;(2)D点的坐标为(6,0);(3)存在.当点C的坐标为(4,2)时,△CBD的周长最小
x2﹣4x+6;(2)D点的坐标为(6,0);(3)存在.当点C的坐标为(4,2)时,△CBD的周长最小
【解析】试题分析:(1)只需运用待定系数法就可求出二次函数的解析式;
(2)只需运用配方法就可求出抛物线的顶点坐标,只需令y=0就可求出点D的坐标;
(3)连接CA,由于BD是定值,使得△CBD的周长最小,只需CD+CB最小,根据抛物线是轴对称图形可得CA=CD,只需CA+CB最小,根据“两点之间,线段最短”可得:当点A、C、B三点共线时,CA+CB最小,只需用待定系数法求出直线AB的解析式,就可得到点C的坐标.
试题解析:
(1)把A(2,0),B(8,6)代入![]() ,得
,得
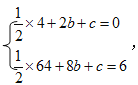
解得:![]()
∴二次函数的解析式为![]() ;
;
(2)由![]() ,得
,得
二次函数图象的顶点坐标为(4,﹣2).
令y=0,得![]() ,
,
解得:x1=2,x2=6,
∴D点的坐标为(6,0);
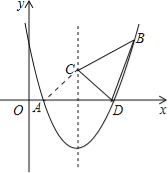
(3)二次函数的对称轴上存在一点C,使得![]() 的周长最小.
的周长最小.
连接CA,如图,
∵点C在二次函数的对称轴x=4上,
∴xC=4,CA=CD,
∴![]() 的周长=CD+CB+BD=CA+CB+BD,
的周长=CD+CB+BD=CA+CB+BD,
根据“两点之间,线段最短”,可得
当点A、C、B三点共线时,CA+CB最小,
此时,由于BD是定值,因此![]() 的周长最小.
的周长最小.
设直线AB的解析式为y=mx+n,
把A(2,0)、B(8,6)代入y=mx+n,得
![]()
解得:![]()
∴直线AB的解析式为y=x﹣2.
当x=4时,y=4﹣2=2,
∴当二次函数的对称轴上点C的坐标为(4,2)时,![]() 的周长最小.
的周长最小.
-
科目: 来源: 题型:
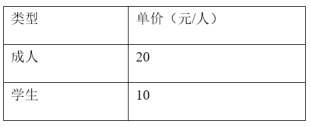
查看答案和解析>>【题目】列方程解应用题:某校组织七年级师生共300人乘车前往“故乡”农场进行劳动教育活动.
(1)他们早晨8:00从学校出发,原计划当天上午10:00便可以到达“故乡”农场,但实际上他们当天上午9:40便达到了“故乡”农场,已知汽车实际行驶速度比原计划行驶速度快10km/h.求汽车原计划行驶的速度.
(2)到达“故乡”农场后,需要购买门票,已知该农场门票票价情况如右表,该校购买门票时共花了3100元,那么参加此次劳动教育的教师、学生各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴如图1,根据给出的数轴,解答下面的问题:

(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数.
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A,B的其它字母表示),并写出这些点表示的数.
(4)折叠纸面.若在数轴上﹣1表示的点与5表示的点重合,回答以下问题:
①10表示的点与数 表示的点重合;
②若数轴上M、N两点之间的距离为2018(M在N的左侧),且M、N两点经折叠后重合,求M、N两点表示的数是多少?
(5)如图2,半径为2的圆周上有一点Q落在数轴上A点处,求将圆在数轴上向右滚动(无滑动)一周后点Q所处的位置的点在数轴上所表示的数.
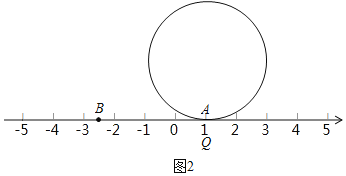
-
科目: 来源: 题型:
查看答案和解析>>【题目】(观察探索)用“<”、“>”或“=”完成以下填空,并观察两边算式,探索规律:
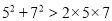
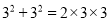
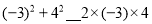
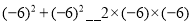
(猜想证明)请用一个含字母a、b的式子表示上以规律,并证明结论的正确性;
(应用拓展)比较代数式m2-3mn+1与mn-4n2的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
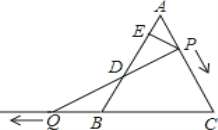
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并解决其后的问题:我们将四个有理数
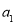 、
、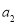 、
、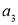 、
、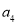 写成
写成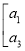
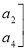 的形式,称它为由有理数
的形式,称它为由有理数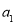 、
、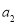 、
、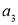 、
、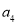 组成的二阶矩阵,称
组成的二阶矩阵,称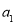 、
、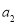 、
、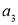 、
、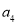 为构成这个矩阵的元素,如由有理数
为构成这个矩阵的元素,如由有理数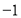 、2、3、
、2、3、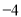 组成的二阶矩阵是
组成的二阶矩阵是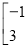
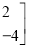 ,
,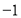 、2、3、
、2、3、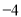 是这个矩阵的元素,当且仅当两个矩阵相同位置上的元素相等时,我们称这两个二阶矩阵相等,下面是两个二阶矩阵的加法运算过程:①
是这个矩阵的元素,当且仅当两个矩阵相同位置上的元素相等时,我们称这两个二阶矩阵相等,下面是两个二阶矩阵的加法运算过程:①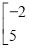
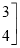 +
+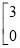
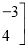 =
=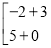
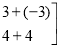 =
=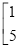
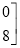 ,②
,②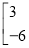
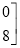 +
+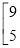
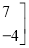 =
=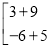
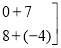 =
=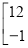
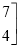 ,
,(1)通过观察上述例子中矩阵加法运算的规律,可归纳得二阶矩阵的加法运算法则是:两个二阶矩阵相加, .
(2)①计算:
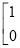
 +
+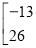
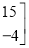 ;
;②若
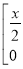
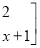 +
+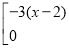
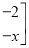 =
=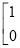
 ,求
,求 的值;
的值;(3)若记A=
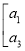
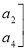 ,B=
,B=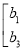
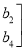 ,试依据二阶矩阵的加法法则说明A+B=B+A成立
,试依据二阶矩阵的加法法则说明A+B=B+A成立
相关试题

