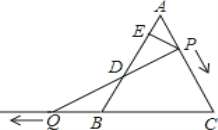
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
参考答案:
【答案】(1)2;(2)证明见解析;(3)3.
【解析】试题分析:(1)先判断出∠QPC是直角,再利用含30°的直角三角形的性质得出QC=2PC,建立方程求解决即可;
(2)先作出PF∥BC得出∠PFA=∠FPA=∠A=60°,进而判断出△DQB≌△DPF得出DQ=DP即可得出结论;
(3)利用等边三角形的性质得出EF=![]() AF,借助DF=DB,即可得出DF=
AF,借助DF=DB,即可得出DF=![]() BF,最后用等量代换即可.
BF,最后用等量代换即可.
试题解析:(1)解:设AP=x,则BQ=x,
∵∠BQD=30°,∠C=60°,
∴∠QPC=90°,
∴QC=2PC,即x+6=2(6-x),
解得x=2,
即AP=2.
(2)证明:如图,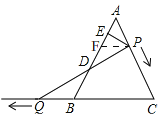
过P点作PF∥BC,交AB于F,
∵PF∥BC,
∴∠PFA=∠FPA=∠A=60°,
∴PF=AP=AF,
∴PF=BQ,
又∵∠BDQ=∠PDF,∠DBQ=∠DFP,
∴△DQB≌△DPF,
∴DQ=DP即D为PQ中点,
(3)运动过程中线段ED的长不发生变化,是定值为3,
理由:∵PF=AP=AF,PE⊥AF,
∴EF=![]() AF,
AF,
又∵△DQB≌△DPF,
∴DF=DB,即DF=![]() BF,
BF,
∴ED=EF+DF=![]() (AF+BF)=
(AF+BF)=![]() AB=3.
AB=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.正数和负数统称为有理数
B.0是最小的有理数
C.如果两个数的绝对值相等,那么这两个数一定相等
D.互为相反数的两个数之和为零
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个数的绝对值相等,那么这两个数( )
A.互为相反数B.相等C.互为相反数或相等D.积为0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标中,点P(-3,2019)在 ( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-xy2)3的结果是( )
A. -x3y6 B. x3y6 C. x4y5 D. -x4y5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°.
(1)将图①中的三角尺绕点O顺时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,则∠CON=________;
(2)将图①中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边MN恰好与射线OC平行;在第________秒时,直线ON恰好平分锐角∠AOC(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.

-
科目: 来源: 题型:
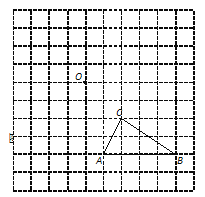
查看答案和解析>>【题目】在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
(1)画出△ABC向左平移2个单位,然后再向上平移4个单位后的△A1B1C1;
(2)画出△A2B2C2,使△A2B2C2和△A1B1C1关于点O成中心对称;
(3)指出如何平移△ABC,使得△A2B2C2和△ABC能拼成一个平行四边形.
相关试题

