【题目】已知在纸面上有一数轴如图1,根据给出的数轴,解答下面的问题:

(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数.
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A,B的其它字母表示),并写出这些点表示的数.
(4)折叠纸面.若在数轴上﹣1表示的点与5表示的点重合,回答以下问题:
①10表示的点与数 表示的点重合;
②若数轴上M、N两点之间的距离为2018(M在N的左侧),且M、N两点经折叠后重合,求M、N两点表示的数是多少?
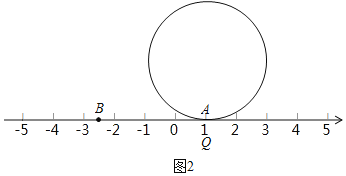
(5)如图2,半径为2的圆周上有一点Q落在数轴上A点处,求将圆在数轴上向右滚动(无滑动)一周后点Q所处的位置的点在数轴上所表示的数.
参考答案:
【答案】(1)A表示的数是1,B表示的数是﹣2.5;
(2)3.5;
(3)-1和3;
(4)①﹣6;②点M为﹣1007,点N为1011.
(5)4π+1.
【解析】
(1)数轴上原点左侧的数为负数,原点右侧的数为正数;
(2)A、B两点间的距离可表示为1-(-2.5),求解即可;
(3)与点A距离为2的点,即A左右两边距离两个单位长度的点,也就是数为1﹣2和1+2的点;
(4)①先求出-1和5的中点,再根据中心对称列式计算即可得解;
②根据中点的定义求出MN的一半,然后分别列式计算即可得解;
(5)先求出圆的周长,再根据平移规律即可得出结论.
解:(1)点A表示的数为1;点B表示的数为﹣2.5;
(2)A、B两点之间的距离为1-(-2.5)=3.5.
(3)在数轴上画出与点A的距离为2的点分别为3和﹣1,即数轴中C和D.
![]()
(4)①(﹣1+5)÷2=2,
2﹣(10﹣2)=﹣6.
故答案为:﹣6;
②∵M、N两点之间的距离为2018,
∴![]() MN=
MN=![]() ×2018=1009,
×2018=1009,
∵对折点的数为2,
∴点M为2﹣1009=﹣1007,点N为2+1009=1011.
(5)∵圆的周长=4π
∴将圆在数轴上向右滚动(无滑动)一周后点Q所处的位置的点在数轴上所表示的数为4π+1.
-
科目: 来源: 题型:
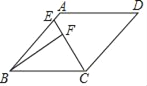
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=45°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为点F.
(1)当点F落在AB上时,求∠BCF的度数;
(2)若∠EBF=15°,求CF的长;
(3)当点E从点A运动到点B时,求点F运动的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=ax﹣a与y=
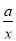 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )A.
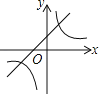 B.
B.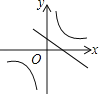
C.
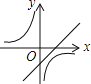 D.
D.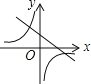
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某校组织七年级师生共300人乘车前往“故乡”农场进行劳动教育活动.
(1)他们早晨8:00从学校出发,原计划当天上午10:00便可以到达“故乡”农场,但实际上他们当天上午9:40便达到了“故乡”农场,已知汽车实际行驶速度比原计划行驶速度快10km/h.求汽车原计划行驶的速度.
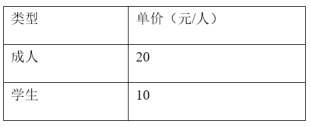
(2)到达“故乡”农场后,需要购买门票,已知该农场门票票价情况如右表,该校购买门票时共花了3100元,那么参加此次劳动教育的教师、学生各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(观察探索)用“<”、“>”或“=”完成以下填空,并观察两边算式,探索规律:
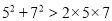
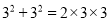
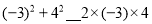
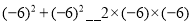
(猜想证明)请用一个含字母a、b的式子表示上以规律,并证明结论的正确性;
(应用拓展)比较代数式m2-3mn+1与mn-4n2的大小,并说明理由.
-
科目: 来源: 题型:
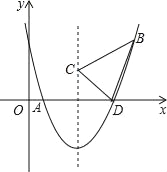
查看答案和解析>>【题目】如图,二次函数y=
 x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
相关试题

