【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,交抛物线于点M,过点C作CF⊥l于F.
(1)求抛物线解析式;
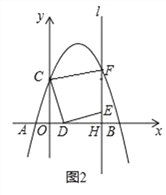
(2)如图2,当点F恰好在抛物线上时(与点M重合)
①求点F的坐标;
②求线段OD的长;
③试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
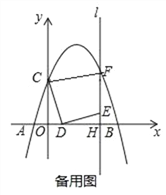
(3)在点D的运动过程中,连接CM,若△COD∽△CFM,请直接写出线段OD的长.

参考答案:
【答案】(1)y=![]() ;(2)①(4,3);②1;
;(2)①(4,3);②1;
③存在,点G的坐标为(4,6)或(4,﹣![]() ).理由见解析;(3)
).理由见解析;(3)![]() 或
或![]() .
.
【解析】分析:(1)先求得点C的坐标,设抛物线的解析式为y=a(x+1)(x﹣5),将点C的坐标代入求得a的值即可;(2)①由题意可知CF∥x轴,则点F纵坐标为3,将y=3代入抛物线的解析式可求得点F的横坐标;②先证明Rt△OCD≌Rt△HDE,从而得到CO=DH=3,然后由OH=4,可得到OD=1;③将CD绕点C逆时针旋转90°得到线段CN,则N(3,4)且四边形CDEN为正方形,然后可求得点N的坐标,接下来求得DG的解析式,然后可求得点G的坐标,由DG⊥DG′以及点D的坐标可求得DG′的解析式,然后可求得点G′的坐标;(3)设点D的坐标为(a,0),则点M的坐标(a+3,﹣![]() a2﹣
a2﹣![]() a+
a+![]() ),然后可求得FM的长,然后由△COD∽△CFM,可得到
),然后可求得FM的长,然后由△COD∽△CFM,可得到![]() ,最后依据上述比例关系列出关于a的方程求解即可.
,最后依据上述比例关系列出关于a的方程求解即可.
本题解析;
(1)把x=0代入抛物线的解析式得:y=3,∴C(0,3).
设抛物线的解析式为y=a(x+1)(x﹣5),将点C的坐标代入得:﹣5a=3,解得:a=﹣![]() .
.
∴抛物线的解析式为y=![]() .
.
(2)①∵CF⊥l,OB⊥l,
∴CF∥x轴.
∴点F的纵坐标为3.
将y=3代入抛物线的解析式得:﹣![]() x2+
x2+![]() x+3=3,解得x=0或x=4.
x+3=3,解得x=0或x=4.
∴点F的坐标为(4,3).
②∵点F的坐标为(4,3),
∴点H的坐标为(4,0).
∵∠CDE=90°,
∴∠CDO+∠EDH=90°.
∵∠OCD+∠CDO=90°,
∴∠OCD=∠EDH.
由旋转的性质可知:CD=DE.
在Rt△OCD和Rt△HDE中, 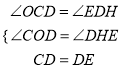 ,
,
∴Rt△OCD≌Rt△HDE.
∴CO=DH=3.
又∵OH=4,
∴OD=1.
③如图1所示:将CD绕点C逆时针旋转90°得到线段CN,则N(3,4)且四边形CDEN为正方形.
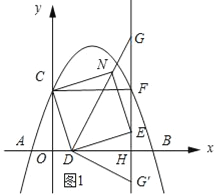
∵四边形CDEN为正方形,
∴∠GDE=45°.
设DN的解析式为y=kx+b,将点D和点N的坐标代入得: ![]() ,解得:k=2,b=﹣2.
,解得:k=2,b=﹣2.
∴DN的解析式为y=2x﹣2.
把x=4代入得:y=6,
∴G(4,6).
设直线DG′的解析式为y=﹣![]() x+c,将点D的坐标代入得:﹣
x+c,将点D的坐标代入得:﹣![]() +c=0,解得:c=
+c=0,解得:c=![]() .
.
∴直线DG′的解析式为y=﹣![]() x+
x+![]() .
.
将x=4代入得:y=﹣![]() .
.
∴点G′的坐标为(4,﹣![]() ).
).
综上所述,点G的坐标为(4,6)或(4,﹣![]() ).
).
(3)如图2所示:
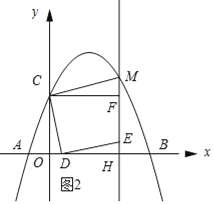
设点D的坐标为(a,0),则点M的坐标(a+3,﹣![]() a2﹣
a2﹣![]() a+
a+![]() ).
).
∴FM=﹣![]() a2﹣
a2﹣![]() a+
a+![]() .
.
∵△COD∽△CFM,
∴![]() ,即
,即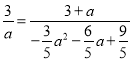 ,
,
整理得:14a2+33a﹣27=0,解得a=![]() 或a=﹣3(舍去).
或a=﹣3(舍去).
∴OD=![]() .
.
如图3所示:
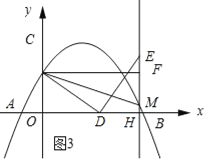
设点D的坐标为(a,0),则点M的坐标(a+3,﹣![]() a2﹣
a2﹣![]() a+
a+![]() ).
).
∴FM=![]() a2+
a2+![]() a﹣
a﹣![]() .
.
∵△COD∽△CFM,
∴![]() ,
, 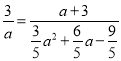 ,整理得:4a2+3a﹣27=9,解得:a=﹣3(舍去)或a=
,整理得:4a2+3a﹣27=9,解得:a=﹣3(舍去)或a=![]() .
.
∴OD=![]() .
.
综上所述,OD的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校1000名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
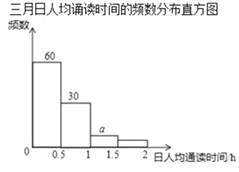
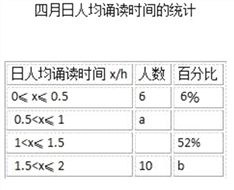
根据以上信息,解答下列问题:
(1)本次调查的学生数为 人;
(2)四月日均诵读时间的统计表中的a值分别为 ;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多 人;
(4)根据抽样调查结果,请你估计该校学生四月份人均诵读时间在1小时以上的人数.
-
科目: 来源: 题型:
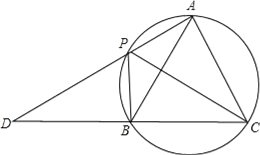
查看答案和解析>>【题目】如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2

①求PD的长.
②图中弧BP和线段DP、BD组成的图形面积为 (结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>0,b<-2,则点(a,b+2)应在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】若线段CD是由线段AB平移得到的,点A(﹣1,3)的对应点为C(2,2),则点B(﹣3,﹣1)的对应点D的坐标是( )
A. (0,﹣2) B. (1,﹣2) C. (﹣2,0) D. (4,6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,逆命题是真命题的是( )
A.直角三角形的两锐角互余
B.对顶角相等
C.若两直线垂直,则两直线有交点
D.若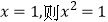
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
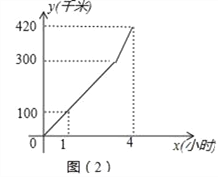
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
相关试题

