【题目】如图,在Rt△ABO中,∠BOA=90°,∠BAO=30°.以AB为一边向上作等边三角形ABE,点D为OA垂直平分线上的一点,且AD⊥AB,连接BD、OD、OE.
(1)判断△ADO的形状,并说明理由;
(2)求证:BD=OE
(3)在射线BA上有一动点P,若△PAO为等腰三角形,直接写出∠AOP的度数

参考答案:
【答案】(1)△ADO是等边三角形,理由见解析;(2)证明见解析;(3)75°或30°或15°.
【解析】
(1)根据AD⊥AB且∠BAO=30°可求出∠DAO=60°,然后根据垂直平分线的性质得到OD=DA,即可证明△ADO是等边三角形;
(2)根据等边三角形的性质结合SAS证明△ABD≌△AEO即可;
(3)分情况讨论:①当OA=AP时,②当OP=AP时,③当OA=AP时,分别根据等腰三角形的性质、三角形内角和定理及三角形外角的性质求解即可.
(1)△ADO是等边三角形;
理由:∵DA⊥BA,∠BAO=30°,
∴∠DAO=90°-30°=60°,
∵点D为OA垂直平分线上的一点,
∴OD=DA,
∴△ADO是等边三角形;
(2)∵△ABE、△ADO是等边三角形,
∴DA=OA,AB=AE,∠OAD=∠EAB=60°,
∵∠BAO=30°,
∴∠BAD=EAO=90°,
∴△ABD≌△AEO(SAS),
∴BD=OE;
(3)分情况讨论:
①当OA=AP时,如图,
∵∠BAO=30°,
∴∠AOP1=(180°-30°)÷2=75°;
②当OP=AP时,如图,
∵∠BAO=30°,
∴∠AOP2=∠BAO=30°;
③当OA=AP时,如图,
∴∠AOP3=∠AP3O,
∵∠BAO=30°,
∴∠AOP3=![]() ∠BAO=15°,
∠BAO=15°,
综上所述:∠AOP的度数为75°或30°或15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
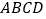 中,
中,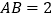 ,
,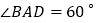 ,过点
,过点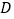 作
作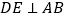 于点
于点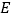 ,
,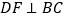 于点
于点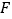 .
. 如图
如图 ,连接
,连接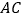 分别交
分别交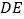 、
、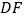 于点
于点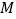 、
、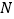 ,求证:
,求证: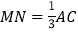 ;
;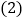 如图
如图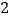 ,将
,将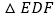 以点
以点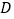 为旋转中心旋转,其两边
为旋转中心旋转,其两边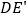 、
、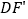 分别与直线
分别与直线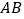 、
、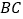 相交于点
相交于点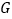 、
、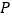 ,连接
,连接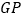 ,当
,当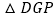 的面积等于
的面积等于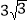 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.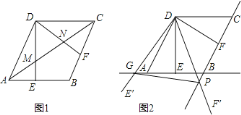
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各个等式的规律:
第一个等式:22-12-1=2,第二个等式:32-22-1=4,第三个等式:42-32-1=6…请用上述等式反映出的规律解决下列问题:
(1)直接写出第四个等式;
(2)猜想第n个等式(用含n的式子表示),并证明你猜想的等式是正确的;
(3)直接写出20202-20192-2019=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,将菱形纸片
,将菱形纸片 沿对角线
沿对角线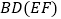 剪开,得到
剪开,得到 和
和 ,固定
,固定 ,并把
,并把 与
与 叠放在一起.
叠放在一起.
 操作:如图
操作:如图 ,将
,将 的顶点
的顶点 固定在
固定在 的
的 边上的中点处,
边上的中点处, 绕点
绕点 在
在 边上方左右旋转,设旋转时
边上方左右旋转,设旋转时 交
交 于点
于点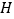 (
(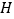 点不与
点不与 点重合),
点重合), 交
交 于点
于点 (
( 点不与
点不与 点重合).
点重合).求证:

 操作:如图
操作:如图 ,
, 的顶点
的顶点 在
在 的
的 边上滑动(
边上滑动( 点不与
点不与 、
、 点重合),且
点重合),且 始终经过点
始终经过点 ,过点
,过点 作
作 ,交
,交 于点
于点 ,连接
,连接 .
.探究:
 ________.请予证明.
________.请予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了看一种图钉落地后钉尖着地的概率有多大,小明作了
 次试验,其中钉尖着地的次数是
次试验,其中钉尖着地的次数是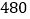 次.下列说法错误的是( )
次.下列说法错误的是( )A. 钉尖着地的频率是
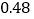
B. 前
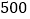 次试验结束后,钉尖着地的次数一定是
次试验结束后,钉尖着地的次数一定是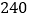 次
次C. 钉尖着地的概率大约是
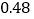
D. 随着试验次数的增加,钉尖着地的频率稳定在
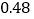
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
相关试题

