【题目】观察下列各个等式的规律:
第一个等式:22-12-1=2,第二个等式:32-22-1=4,第三个等式:42-32-1=6…请用上述等式反映出的规律解决下列问题:
(1)直接写出第四个等式;
(2)猜想第n个等式(用含n的式子表示),并证明你猜想的等式是正确的;
(3)直接写出20202-20192-2019=
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)2020.
,证明见解析;(3)2020.
【解析】
(1)根据所给等式,可直接写出第四个等式;
(2)观察所给等式可得:等号左边的第一个数是序号加1的平方,第二个数是序号的平方,第三个数是1,等号右边是序号的二倍,据此写出第n个等式,然后展开证明即可;
(3)利用(2)中等式先求出20202-20192的值,然后即可求出结果.
(1)由题意得,第四个等式为:![]() ;
;
(2)观察所给等式可得:等号左边的第一个数是序号加1的平方,第二个数是序号的平方,第三个数是1,等号右边是序号的二倍,
故猜想第n个等式为:![]() ,
,
证明:左边=![]() =右边,
=右边,
故等式成立;
(3)∵![]() ,
,
∴![]() ,
,
∴20202-20192=2×2019+1,
∴20202-20192-2019=2×2019+1-2019=2020.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, .
.⑴已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:
 ;
;⑵以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若
 ,求
,求 的度数.
的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
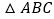 为等边三角形,点
为等边三角形,点 为直线
为直线 上的一动点(点
上的一动点(点 不与
不与 、
、 重合),以
重合),以 为边作菱形
为边作菱形 (
( 、
、 、
、 、
、 按逆时针排列),使
按逆时针排列),使 ,连接
,连接 .
. 如图
如图 ,当点
,当点 在边
在边 上时,求证:①
上时,求证:① ;②
;② ;
; 如图
如图 ,当点
,当点 在边
在边 的延长线上且其他条件不变时,结论
的延长线上且其他条件不变时,结论 是否成立?若不成立,请写出
是否成立?若不成立,请写出 、
、 、
、 之间存在的数量关系,并说明理由;
之间存在的数量关系,并说明理由; 如图
如图 ,当点
,当点 在边
在边 的延长线上且其他条件不变时,补全图形,并直接写出
的延长线上且其他条件不变时,补全图形,并直接写出 、
、 、
、 之间存在的数量关系.
之间存在的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
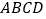 中,
中,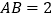 ,
,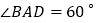 ,过点
,过点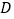 作
作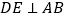 于点
于点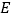 ,
,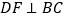 于点
于点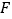 .
.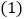 如图
如图 ,连接
,连接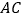 分别交
分别交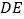 、
、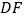 于点
于点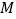 、
、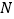 ,求证:
,求证: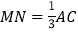 ;
;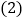 如图
如图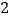 ,将
,将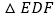 以点
以点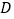 为旋转中心旋转,其两边
为旋转中心旋转,其两边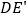 、
、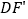 分别与直线
分别与直线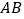 、
、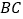 相交于点
相交于点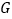 、
、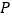 ,连接
,连接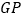 ,当
,当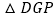 的面积等于
的面积等于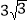 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.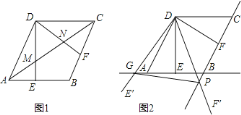
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,将菱形纸片
,将菱形纸片 沿对角线
沿对角线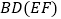 剪开,得到
剪开,得到 和
和 ,固定
,固定 ,并把
,并把 与
与 叠放在一起.
叠放在一起.
 操作:如图
操作:如图 ,将
,将 的顶点
的顶点 固定在
固定在 的
的 边上的中点处,
边上的中点处, 绕点
绕点 在
在 边上方左右旋转,设旋转时
边上方左右旋转,设旋转时 交
交 于点
于点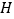 (
(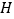 点不与
点不与 点重合),
点重合), 交
交 于点
于点 (
( 点不与
点不与 点重合).
点重合).求证:

 操作:如图
操作:如图 ,
, 的顶点
的顶点 在
在 的
的 边上滑动(
边上滑动( 点不与
点不与 、
、 点重合),且
点重合),且 始终经过点
始终经过点 ,过点
,过点 作
作 ,交
,交 于点
于点 ,连接
,连接 .
.探究:
 ________.请予证明.
________.请予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABO中,∠BOA=90°,∠BAO=30°.以AB为一边向上作等边三角形ABE,点D为OA垂直平分线上的一点,且AD⊥AB,连接BD、OD、OE.
(1)判断△ADO的形状,并说明理由;
(2)求证:BD=OE
(3)在射线BA上有一动点P,若△PAO为等腰三角形,直接写出∠AOP的度数

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

相关试题

