【题目】如图,点A(2,2 ![]() ),N(1,0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为.
),N(1,0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为.
参考答案:
【答案】![]()
【解析】如图,过点A作AB⊥x轴,
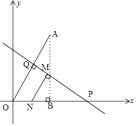
则OB=2、AB=2 ![]() ,
,
∴OA= ![]() ,
,
∵cos∠AOB= ![]() ,
,
∴∠AOB=60°,
作AO的中垂线交x轴于点P,交OA于点Q,
则OQ=AQ=2,
∴OP= ![]() =4,
=4,
∵N(1,0),
∴PN=3,
∵MO=MA,
∴点M在PQ上,
当MN⊥PQ时,MN最小,
∵PQ⊥OA、PQ⊥MN,
∴△PMN∽△PQO,
∴ ![]() ,即
,即 ![]() ,
,
解得:MN= ![]() ,
,
故答案为: ![]() .
.
根据勾股定理求出OA的值,再根据三角函数得到∠AOB的度数,由MO=MA,得到点M在OA的垂直平分线上,得到△PMN∽△PQO,求出MN的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
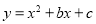 的图像与
的图像与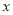 轴交于
轴交于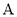 、
、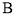 两点,与
两点,与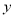 轴交于点
轴交于点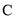 ,
,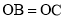 .点
.点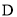 在函数图像上,
在函数图像上,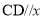 轴,且
轴,且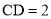 ,直线
,直线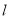 是抛物线的对称轴,
是抛物线的对称轴,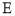 是抛物线的顶点.
是抛物线的顶点.(1)求
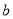 、
、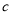 的值;
的值;(2)如图①,连接
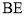 ,线段
,线段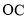 上的点
上的点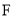 关于直线
关于直线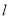 的对称点
的对称点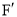 恰好在线段
恰好在线段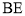 上,求点
上,求点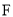 的坐标;
的坐标;(3)如图②,动点
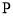 在线段
在线段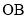 上,过点
上,过点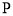 作
作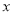 轴的垂线分别与
轴的垂线分别与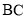 交于点
交于点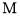 ,与抛物线交于点
,与抛物线交于点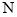 .试问:抛物线上是否存在点
.试问:抛物线上是否存在点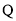 ,使得
,使得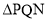 与
与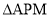 的面积相等,且线段
的面积相等,且线段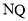 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点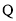 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.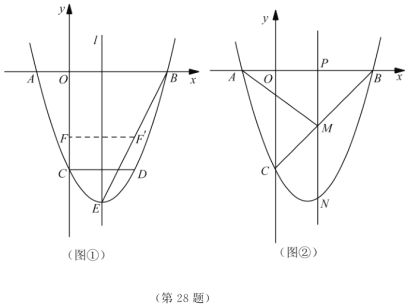
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a3÷a2=a
B.a2+a2=a4
C.(2a+b)2=4a2+b2+4ab
D.(2a+1)(2a﹣1)=2a2﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分)
70
80
90
男生(人)
5
10
7
女生(人)
4
13
4
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系XOY中,A(-1,5),B(-1,0),C(-4,3).
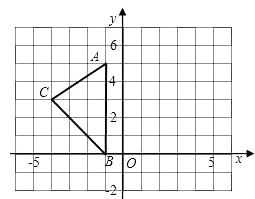
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.

(1)求证: AE=AF;
(2)若AG=4,AC=7,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
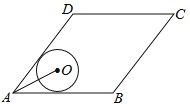
A.5 B.6 C.2
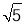 D.3
D.3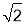
相关试题

