【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.
(1)求证: AE=AF;
(2)若AG=4,AC=7,求FG的长.
参考答案:
【答案】
(1)解:∵BF平分∠ABC
∴∠ABF=∠CBF
∵∠AFB=180°-∠ABF-∠BAF
∠BED=180°-∠CBF-∠ADB
又∵∠BAC=∠ADB
∴∠AFB=∠BED
∵∠AEF=∠BED
∴∠AFB=∠AEF
∴AE=AF
(2)解:如图,在BC上截取BH=AB,连接FH

在△ABF和△HBF中
∵ 
∴△ABF≌△HBF(SAS)
∴AF=FH,∠AFB=∠HFB
∵∠AFB=∠AEF
∴∠HFB=∠AEF
∴AE∥FH
∴∠GAE=∠CFH
∵EG∥BC
∴∠AGE=∠C
∵AE=AF
∴AE=FH
在△AEG和△FHC中
∵ 
∴△AEG≌△FHC(AAS)
∴AG=FC=4
∴FG=AG+ FC -AC=1
【解析】(1)根据角平分线性质和三角形内角和定理,∠AFB=∠BED,再根据对顶角相等,得到∠AFB=∠AEF,根据等角对等边得到AE=AF;(2)根据全等三角形的判定方法SAS,得到△ABF≌△HBF,得到对应边、对应角相等;再由EG∥BC,根据AAS得到△AEG≌△FHC,得到对应边AG=FC,求出FG=AG+ FC -AC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分)
70
80
90
男生(人)
5
10
7
女生(人)
4
13
4
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(2,2
 ),N(1,0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为.
),N(1,0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系XOY中,A(-1,5),B(-1,0),C(-4,3).
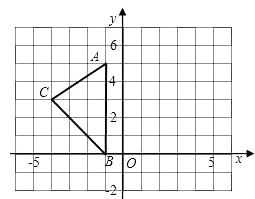
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
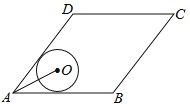
A.5 B.6 C.2
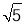 D.3
D.3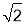
-
科目: 来源: 题型:
查看答案和解析>>【题目】50°角的余角是_____,补角是_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个内角都等于140°,则这个多边形的边数是( )
A.7
B.8
C.9
D.10
相关试题

