【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .点
.点![]() 在函数图像上,
在函数图像上,![]() 轴,且
轴,且![]() ,直线
,直线![]() 是抛物线的对称轴,
是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求![]() 、
、![]() 的值;
的值;
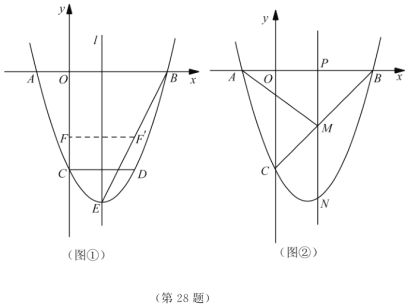
(2)如图①,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)如图②,动点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线分别与
轴的垂线分别与![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等,且线段
的面积相等,且线段![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 和
和![]()
【解析】
试题分析: (1)根据二次函数的对称轴公式,抛物线上的点代入,即可;(2)先求F的对称点,代入直线BE,即可;(3)构造新的二次函数,利用其性质求极值.
试题解析:.解:(1)![]() 轴,
轴,![]() ,
,![]() 抛物线对称轴为直线
抛物线对称轴为直线![]()
![]()
![]() 点的坐标为
点的坐标为![]()
![]() 解得
解得![]() 或
或![]() (舍去),
(舍去),![]()
(2)设点![]() 的坐标为
的坐标为![]()
![]() 对称轴为直线
对称轴为直线![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() .
.
![]() 直线
直线![]() 经过点
经过点![]() 利用待定系数法可得直线
利用待定系数法可得直线![]() 的表达式为
的表达式为![]() .
.
因为点![]() 在
在![]() 上,
上,![]()
![]() 即点
即点![]() 的坐标为
的坐标为![]()
(3)存在点![]() 满足题意.设点
满足题意.设点![]() 坐标为
坐标为![]() ,则
,则![]()
作![]() 垂足为
垂足为![]()
![]()
![]()
①点![]() 在直线
在直线![]() 的左侧时,
的左侧时,![]() 点的坐标为
点的坐标为![]() 点的坐标为
点的坐标为![]() 点的坐标为
点的坐标为![]()
![]() 在
在![]() 中,
中,![]() 时,
时,![]() 取最小值
取最小值![]() .此时
.此时![]() 点的坐标为
点的坐标为![]()
②点![]() 在直线
在直线![]() 的右侧时,
的右侧时,![]() 点的坐标为
点的坐标为![]() 同理,
同理,![]() 时,
时,![]() 取最小值
取最小值![]() .此时
.此时![]() 点的坐标为
点的坐标为![]()
综上所述:满足题意得点![]() 的坐标为
的坐标为![]() 和
和![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC与△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )
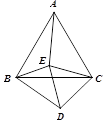
A.115°
B.120°
C.125°
D.130° -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2a2﹣2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D在AC上,且BD=AD, ∠A=36°,则∠DBC=.
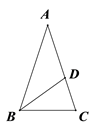
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a3÷a2=a
B.a2+a2=a4
C.(2a+b)2=4a2+b2+4ab
D.(2a+1)(2a﹣1)=2a2﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分)
70
80
90
男生(人)
5
10
7
女生(人)
4
13
4
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(2,2
 ),N(1,0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为.
),N(1,0), ∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为.
相关试题

