【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

参考答案:
【答案】(1)证明见解析;(2)CG=![]() ;(3)∠EFC=120°或30°.
;(3)∠EFC=120°或30°.
【解析】分析: (1)作EP⊥CD于P,EQ⊥BC于Q,证明Rt△EQF≌Rt△EPD,得到EF=ED,根据正方形的判定定理证明即可;
(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解决问题.
(3)分两种情形考虑问题即可
详解:
(1)证明:作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
 ,
,
∴Rt△EQF≌Rt△EPD,
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中.AC=![]() AB=2
AB=2![]() ,
,
∵EC=![]() ,
,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=![]() .
.
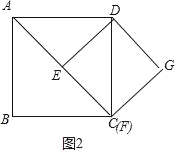
(3)①当DE与AD的夹角为30°时,∠EFC=120°,
②当DE与DC的夹角为30°时,∠EFC=30°
综上所述,∠EFC=120°或30°.
点睛: 本题考查正方形的性质、矩形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知k是不等于0的常数,反比例函数与二次函数在同一坐标系的大致图象如图,则它们的解析式可能分别是( )
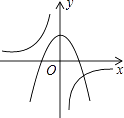
A.y=﹣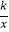 ,y=﹣kx2+k
,y=﹣kx2+k
B.y=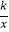 ,y=﹣kx2+k
,y=﹣kx2+k
C.y=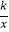 ,y=kx2+k
,y=kx2+k
D.y=﹣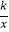 ,y=﹣kx2﹣k
,y=﹣kx2﹣k -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,各正方形的边长均为1,则四个阴影三角形中,一定相似的一对是( )

A.①②
B.①③
C.②③
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
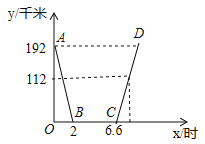
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
-
科目: 来源: 题型:
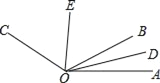
查看答案和解析>>【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线相交,只有1个交点,三条直线相交,最多有3个交点,四条直线相交,最多有6个交点,10条直线相交,最多有( )个交点.
A. 45 B. 42 C. 40 D. 36
相关试题

