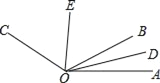
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
参考答案:
【答案】(1) 65°’;(2) 150°;(3) ∠DOE=![]() ∠AOC,理由见解析
∠AOC,理由见解析
【解析】
(1)利用角平分线的定义得出∠AOD=∠BOD,∠BOE=∠COE,进而求出∠DOE的度数;
(2)根据角平分线的定义求出∠DOB和∠EOB的度数,代入∠DOE=∠DOB+∠EOB求出即可;
(3)根据角的和差关系求出∠AOC度数,再根据角平分线的定义求出∠DOB和∠EOB,代入∠DOE=![]() ∠BOC+∠AOB得出关系即可.
∠BOC+∠AOB得出关系即可.
(1)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∵∠BOC=50°,∠BOA=80°,
∴∠BOD=25°,∠BOE=40°,
∴∠DOE=25°+40°=65°;
(2)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∵∠AOC=150°,
∴∠DOE=∠DOB+∠EOB=![]() (∠BOC+∠BOA)=
(∠BOC+∠BOA)=![]() ∠AOC=75°;
∠AOC=75°;
(3)∠DOE=![]() ∠AOC;
∠AOC;
理由是:∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∴∠DOE=∠DOB+∠EOB=![]() (∠BOC+∠BOA)=
(∠BOC+∠BOA)=![]() ∠AOC.
∠AOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
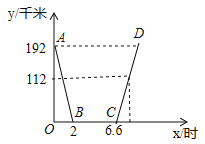
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=
 ,求CG的长度;
,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线相交,只有1个交点,三条直线相交,最多有3个交点,四条直线相交,最多有6个交点,10条直线相交,最多有( )个交点.
A. 45 B. 42 C. 40 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OE是∠AOD的平分线,OC是∠BOD的平分线.
(1)若∠AOB=130°,则∠COE是多少度?
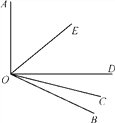
(2)在(1)的条件下,若∠COD=20°,则∠BOE是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E,F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )

A.
B.
C.
D.
相关试题

