搜索
【题目】如图，各正方形的边长均为1，则四个阴影三角形中，一定相似的一对是（ ） 
A.①②
B.①③
C.②③
D.②④
参考答案：
【答案】A
【解析】解：①三边长为：1， 
， 
；
②三边长为： ，2， 
；
③三边长为：1， ，2 ；
④三边长为：2， ， 
；
则可得①和②三边成比例，故一定相似的是①和②．
故选A．
【考点精析】本题主要考查了勾股定理的概念和相似三角形的判定的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点A，O，B依次在直线MN上，如图1，现将射线OA绕点O顺时针方向以每秒10°的速度旋转，同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转，直线MN保持不动，如图2，设旋转时间为t秒（t≤12）．
（1）在旋转过程中，当t=2时，求∠AOB的度数．
（2）在旋转过程中，当∠AOB=105°时，求t的值．
（3）在旋转过程中，当OA或OB是某一个角（小于180°）的角平分线时，求t的值．
-
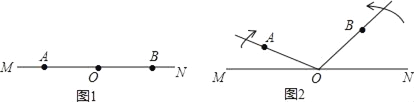
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，⊙O的半径为1，P是坐标系内任意一点，点P到⊙O的距离SP的定义如下：若点P与圆心O重合，则SP为⊙O的半径长；若点P与圆心O不重合，作射线OP交⊙O于点A，则SP为线段AP的长度． 图1为点P在⊙O外的情形示意图．
（1）若点B（1，0），C（1，1），
，则SB=；SC=；SD=；
（2）若直线y=x+b上存在点M，使得SM=2，求b的取值范围；
（3）已知点P，Q在x轴上，R为线段PQ上任意一点．若线段PQ上存在一点T，满足T在⊙O内且ST≥SR ， 直接写出满足条件的线段PQ长度的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知k是不等于0的常数，反比例函数与二次函数在同一坐标系的大致图象如图，则它们的解析式可能分别是（ ）
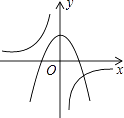
A.y=﹣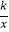
，y=﹣kx2+k
B.y=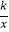 ，y=﹣kx2+k
C.y=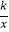 ，y=kx2+k
D.y=﹣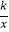 ，y=﹣kx2﹣k -
科目： 来源： 题型：
查看答案和解析>>【题目】昨天早晨7点，小明乘车从家出发，去西安参加中学生科技创新大赛，赛后，他当天按原路返回，如图，是小明昨天出行的过程中，他距西安的距离y（千米）与他离家的时间x（时）之间的函数图象．
根据下面图象，回答下列问题：
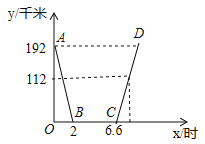
（1）求线段AB所表示的函数关系式；
（2）已知昨天下午3点时，小明距西安112千米，求他何时到家？
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
（1）如图1，求证：矩形DEFG是正方形；
（2）若AB=2，CE=
，求CG的长度；（3）当线段DE与正方形ABCD的某条边的夹角是30°时，直接写出∠EFC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】平行四边形ABCD中，E，F是对角线BD上的两点， 如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（ ）
A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
相关试题
