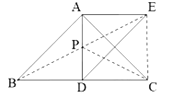
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是中线,作
是中线,作![]() 关于
关于![]() 的轴对称图形
的轴对称图形![]() .
.
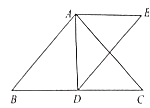
(1)直接写出![]() 和
和![]() 的位置关系;
的位置关系;
(2)连接![]() ,写出
,写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() ,
,![]() 时,在
时,在![]() 上找一点
上找一点![]() ,使得点
,使得点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最下小,求
的距离之和最下小,求![]() 的面积.
的面积.
参考答案:
【答案】(1)垂直;(2)![]() .理由见解析;(3)
.理由见解析;(3)![]() .
.
【解析】
(1)根据对称点连线垂直于对称轴,即可确定AC⊥DE;(2)连接CE,证明四边形AECD是正方形,在结合三角形ABC是等腰三角形,即可说明;(3)先证明.△ACD≌△ABD,得到点B和点C关于AD成轴对称;连接![]() ,交
,交![]() 于点
于点![]() ,且当
,且当![]() ,
,![]() ,
,![]() 三点在同一条直线上,点
三点在同一条直线上,点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最小,然后结合(1)的结论,运用三角形的面积公式即可求得.
的距离之和最小,然后结合(1)的结论,运用三角形的面积公式即可求得.
解:(1)垂直
(2)![]() .理由如下:
.理由如下:
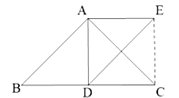
![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
![]() ,
,![]()
在![]() 和
和![]() 中,
中,
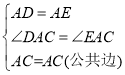
![]()
![]()
又![]() 是边
是边![]() 上的中线
上的中线
![]() .
.
![]() .
.
(3)在![]() 和
和![]() 中
中
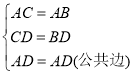
![]()
![]()
![]()
![]()
![]() 点
点![]() 和点
和点![]() 关于
关于![]() 成轴对称
成轴对称
连接![]() ,交
,交![]() 于点
于点![]() ,如图所示
,如图所示
![]()
![]()
且当![]() ,
,![]() ,
,![]() 三点在同一条直线上,点
三点在同一条直线上,点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最小
的距离之和最小
![]()
![]()
在![]() 中,.
中,.![]()
由(1)知,![]() ,
,
![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD的对角线交于O点,一条边的长为1,△AOB是正三角形,则这个矩形的周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=
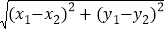 ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上
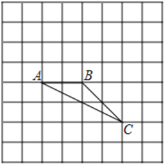
(1) 填空∠ABC=___________
(2) 若点A在网格所在的坐标平面内的坐标为(1,-2),请建立平面直角坐标系,D是平面直角坐标系中一点,并作出以A、B、C、D四个点为顶点的平行四边形,直接写出满足条件的D点的坐标
-
科目: 来源: 题型:
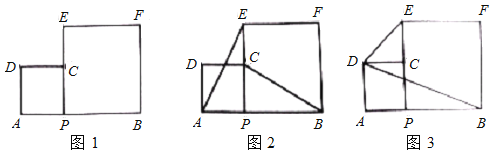
查看答案和解析>>【题目】已知,AB=18,动点P从点A出发,以每秒1个单位的速度向点B运动,分别以AP、BP为边在AB的同侧作正方形。设点P的运动时间为t.
(1)如图1,若两个正方形的面积之和
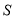 ,
,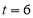 当时,求出
当时,求出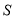 的大小;
的大小;(2)如图2,当
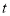 取不同值时,判断直线
取不同值时,判断直线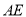 和
和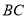 的位置关系,说明理由;
的位置关系,说明理由;(3)如图3,用
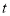 表示出四边形
表示出四边形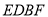 的面积
的面积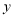 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月12日,安庆“筑梦号”自动驾驶公开试乘体验正式启动,让安庆成为全国率先开通自动驾驶的城市,智能、绿色出行的时代即将到来.普通燃油车从A地到B地,所需油费108元,而自动驾驶的纯电动车所需电费27元,已知每行驶l千米,普通燃油汽车所需的油费比自动的纯电动汽车所需的电费多0.54元,求自动驾驶的纯电动汽车每行驶1千米所需的电费.
-
科目: 来源: 题型:
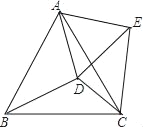
查看答案和解析>>【题目】如图,在等边△ABC 内有一点D,AD=5,BD=6,CD=4,将线段AD绕点A旋转到AE,使∠DAE=∠BAC,连接EC.
(1)求CE的长;
(2)求cos∠CDE的值.
相关试题

