【题目】矩形ABCD的对角线交于O点,一条边的长为1,△AOB是正三角形,则这个矩形的周长为________.
参考答案:
【答案】2+![]() 或
或![]() .
.
【解析】
画出图形,根据矩形的对角线互相平分且相等可得AC=2OB,再根据等边三角形的三边都相等,然后求出AC=2AB,然后分①AB=1时,利用勾股定理列式求出BC,②BC=1时,利用勾股定理列式求出AB的长,再根据矩形的周长公式列式计算即可得解.
解:在矩形ABCD中,AC=2OB,
∵△AOB是正三角形,
∴OB=AB,
∴AC=2AB,
①AB=1时,AC=2,
根据勾股定理,BC=![]() ,
,
所以,矩形的周长=2(AB+BC)=2(1+![]() )=2+2
)=2+2![]() ;
;
②BC=1时,根据勾股定理,AB2+BC2=AC2,
所以,AB2+12=(2AB)2,
解得AB=![]() ,
,
所以,矩形的周长=2(AB+BC)=2(![]() +1)=
+1)=![]() +2;
+2;
综上所述,矩形的周长为2+2![]() 或
或![]() +2.
+2.
故答案为:2+2![]() 或
或![]() +2.
+2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
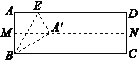

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, .
.
(1)用尺规作图法作
 ,与边
,与边 交于点
交于点 (保留作题痕迹,不用写作法);
(保留作题痕迹,不用写作法);(2)在(1)的条件下,当
 时,求
时,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=
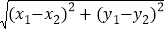 ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.已知一个三角形各顶点坐标为D(1,6)、E(4,2),平面直角坐标系中,在x轴上找一点P,使PD+PE的长度最短,则PD+PE的最短长度为__________ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上
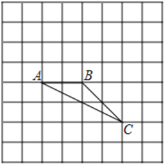
(1) 填空∠ABC=___________
(2) 若点A在网格所在的坐标平面内的坐标为(1,-2),请建立平面直角坐标系,D是平面直角坐标系中一点,并作出以A、B、C、D四个点为顶点的平行四边形,直接写出满足条件的D点的坐标
-
科目: 来源: 题型:
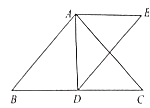
查看答案和解析>>【题目】如图,在
 中,
中, ,
,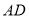 是中线,作
是中线,作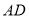 关于
关于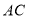 的轴对称图形
的轴对称图形 .
.
(1)直接写出
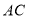 和
和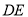 的位置关系;
的位置关系;(2)连接
 ,写出
,写出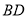 和
和 的数量关系,并说明理由;
的数量关系,并说明理由;(3)当
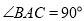 ,
,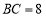 时,在
时,在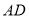 上找一点
上找一点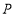 ,使得点
,使得点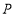 到点
到点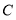 与到点
与到点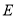 的距离之和最下小,求
的距离之和最下小,求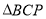 的面积.
的面积.
相关试题

