搜索
【题目】完成下面的证明过程：
已知：如图，∠D=110°，∠EFD=70°，∠1=∠2，
求证：∠3=∠B
证明：∵∠D=110°, ∠EFD=70°（已知）
∴∠D+∠EFD=180°
∴AD∥______（ ）
又∵∠1=∠2(已知)
∴_____∥BC ( 内错角相等，两直线平行)
∴EF∥_____ ( )
∴∠3=∠B(两直线平行，同位角相等)
参考答案：
【答案】详见解析.
【解析】
求出∠D+∠EFD=180°，根据平行线的判定推出AD∥EF，AD∥BC，即可推出答案．
证明：∵∠D=110°, ∠EFD=70°（已知）
∴∠D+∠EFD=180°
∴AD∥_EF_（ 同旁内角互补，两直线平行 ）
又∵∠1=∠2(已知)
∴AD∥BC ( 内错角相等，两直线平行)
∴EF∥_BC_ ( 平行于同一直线的两直线平行 )
∴∠3=∠B(两直线平行，同位角相等) ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】列分式方程解应用题
元旦期间，甲、乙两位好友约着一起开两辆车自驾去黄山玩，其中面包车为领队，小轿车紧随其后，他们同时出发，当面包车行驶了200千米时，发现小轿车只行驶了180千米，若面包车的行驶速度比小轿车快10千米/小时,请问：
（1）小轿车和面包车的速度分别多少？
（2）当小轿车发现落后时，为了追上面包车，他就马上提速，面包车速度不变，他们约定好在面包车前面100千米的地方碰头，他们正好同时到达，请问小轿车需要提速多少千米/小时？
（3）小轿车发现落后时，为了追上面包车，他就马上提速，面包车速度不变，他们约定好在面包车前面s千米的地方碰头，他们正好同时到达，请问小轿车提速 千米/小时．（请你直接写出答案即可）
-
科目： 来源： 题型：
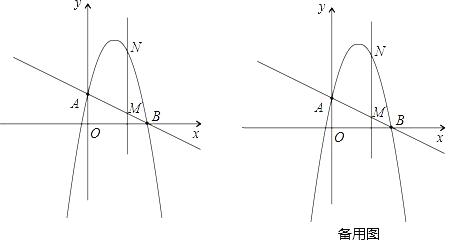
查看答案和解析>>【题目】如图，一次函数
分别交y轴、x轴于A、B两点，抛物线y=﹣x2+bx+c过A、B两点．（1）求这个抛物线的解析式；
（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？
（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：
如图1，已知：在
中，
，
，直线m经过点A，
直线m，
直线m，垂足分别为点D、
试猜想DE、BD、CE有怎样的数量关系，请直接写出；
组员小颖想，如果三个角不是直角，那结论是否会成立呢？如图2，将中的条件改为：在中，，D、A、E三点都在直线m上，并且有
其中
为任意锐角或钝角
如果成立，请你给出证明；若不成立，请说明理由．
数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，F是
角平分线上的一点，且
和
均为等边三角形，D、E分别是直线m上A点左右两侧的动点
、E、A互不重合
，在运动过程中线段DE的长度始终为n，连接BD、CE，若
，试判断
的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O为正方形ABCD的中心，BE平分∠DBC交DC于点E，延长BC到点F，使FC=EC，连结DF交BE的延长线于点H，连结OH交DC于点G，连结HC．则以下四个结论中：①OH∥BF，②GH=
BC，③BF=2OD，④∠CHF=45°．正确结论的个数为( )
A.4个B.3个C.2个D.1个
-
科目： 来源： 题型：
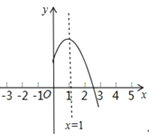
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图所示，对于下列说法：①abc＜0；②a﹣b+c＜0；③3a+c＜0；④当﹣1＜x＜3时，y＞0．其中正确的是______（把正确说法的序号都填上）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD．
（1）若AB=2，OD=3，求BC的长；
（2）若作直线CD，试说明直线CD是⊙O的切线．
相关试题
