【题目】如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD.
(1)若AB=2,OD=3,求BC的长;
(2)若作直线CD,试说明直线CD是⊙O的切线.

参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)求出![]() ,
, ![]() ,
, ![]() ,推出
,推出![]() 代入求出即可;
代入求出即可;
(2)求出![]() 证
证![]() ≌
≌![]() ,推出
,推出![]() ,即可得出答案.
,即可得出答案.
试题解析:(1)∵AB是![]() 的直径,AD是
的直径,AD是![]() 的切线,
的切线,
![]()
∵BC![]() OD,
OD,
∴∠B=∠DOA,
∵∠ACB=∠DAO,∠B=∠DOA,
∴△ABC∽△DOA,
![]()
∵AB=2,OD=3,OA=1,
![]()
解得: ![]()
(2)证明:连接OC,

∵BC![]() OD,
OD,
∴∠B=∠AOD,∠BCO=∠COD,
∵OC=OB,
∴∠BCO=∠OBC,
∴∠COD=∠AOD,
∵在△DOC和△DOA中

∴△DOC≌△DOA,
∴∠OCD=∠OAD,
![]()
![]()
∵OC是半径,
∴DC是![]() 的切线.
的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程:
已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,
求证:∠3=∠B

证明:∵∠D=110°, ∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥______( )
又∵∠1=∠2(已知)
∴_____∥BC ( 内错角相等,两直线平行)
∴EF∥_____ ( )
∴∠3=∠B(两直线平行,同位角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=
 BC,③BF=2OD,④∠CHF=45°.正确结论的个数为( )
BC,③BF=2OD,④∠CHF=45°.正确结论的个数为( )
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
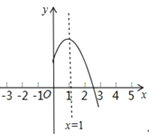
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中正确的是______(把正确说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=4,OC=10,∠A=60°,线段EF垂直平分OD,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E'关于x轴对称,连接BP、E'M,则BP+PM+ME'的长度的最小值为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的三个数值为﹣7,﹣1,3.乙袋中的三张卡片上所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上的数值,把x,y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况;
(2)求点A落在反比例函数
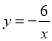 图象上的概率.
图象上的概率.
相关试题

