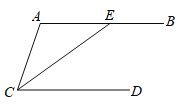
【题目】如图,∠ACE=∠AEC.
(1)若CE平分∠ACD,求证:AB∥CD.
(2)若AB∥CD,求证:CE平分∠ACD.请在(1)、(2)中选择一个进行证明.
参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据等量代换得到∠ACE=∠AEC,再根据平行线的判定,即可得出AB∥CD;
(2)根据等量代换得到∠ACE=∠ECD,再根据角平分线的定义,即可得出CE平分∠ACD.
解:(1)∵CE平分∠ACD.(已知)
∴∠ACE=∠ECD.(角平线定义)
∵∠ACE=∠AEC.(已知)
∴∠ECD=∠AEC.(等量代换)
∴AB∥CD.(内错角相等,两直线平行)
(2)∵AB∥CD.(已知)
∴∠AEC=∠ECD.(两直线平行,内错角相等)
∵∠ACE=∠AEC.(已知)
∴∠ACE=∠ECD.(等量代换)
∴CE平分∠ACD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
态度
A.顾客出面制止
B.劝说进吸烟室
C.超市老板出面制止
D.无所谓
频数(人数)
90
30
10
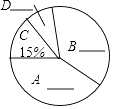
请你根据统计图、表提供的信息解答下列问题:
(1)这次抽样的公众有人.
(2)请将统计表和扇形统计图补充完整;
(3)在统计图中“B”部分所对应的圆心角是度.
(4)若该市有120万人,估计该市态度为“A.顾客出面制止”的有万人. -
科目: 来源: 题型:
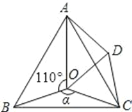
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
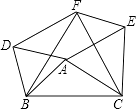
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣8,4)、(2,﹣8),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以
 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的
 ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.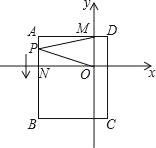
-
科目: 来源: 题型:
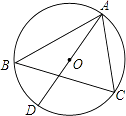
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD是⊙O直径,若∠ABC=50°,则∠CAD=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简或求值
(1)若A=-2a2+ab-b3,B=a2-2ab+b3,求A -2B的值。
(2)先化简,再求值:5x2y-3xy2-7(x2y- xy
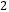 ),其中x=2,y=-1。
),其中x=2,y=-1。
相关试题

