【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.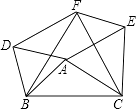
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在.
参考答案:
【答案】
(1)证明:∵△ABD和△FBC都是等边三角形,
BD=BA,BF=BC,∠DBA=∠FBC=60°,
∴∠DBA﹣∠FBA=∠FBC﹣∠FBA,
∴∠DBF=∠ABC.
在△ABC和△DBF中, 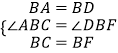
∴△ABC≌△DBF.
∴AC=DF=AE.
同理△ABC≌△EFC.
∴AB=EF=AD.
∴四边形ADFE是平行四边形.
(2)∠BAC=150°,AB=AC≠BC,∠BAC=60°
【解析】解:(2)当∠BAC=150°,∠DAE=360°﹣60°﹣60°﹣150°=90°,
∴平行四边形DAEF是矩形.
当AB=AC≠BC,有AD=AE,
∴平行四边形DAEF是菱形.
当∠BAC=60°,D、A、E、F四点共线,四边形不存在.
【考点精析】本题主要考查了等边三角形的性质和平行四边形的判定的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点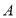 的坐标分
的坐标分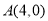 ,点
,点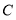 的坐标为
的坐标为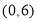 ,点
,点 在第一象限内,点
在第一象限内,点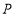 从原点出发,以每秒2个单位长度的速度沿着
从原点出发,以每秒2个单位长度的速度沿着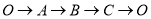 的路线移动(即沿着长方形移动一周).
的路线移动(即沿着长方形移动一周).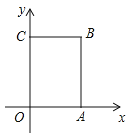
(1)写出点
 的坐标;
的坐标;(2)当点
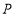 移动了4秒时,求出点
移动了4秒时,求出点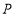 的坐标.
的坐标.(3)在移动过程中,当点
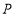 到
到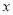 轴的距离为5个单位长度时,求点
轴的距离为5个单位长度时,求点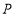 移动的时间.
移动的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】“戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
态度
A.顾客出面制止
B.劝说进吸烟室
C.超市老板出面制止
D.无所谓
频数(人数)
90
30
10
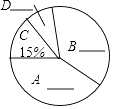
请你根据统计图、表提供的信息解答下列问题:
(1)这次抽样的公众有人.
(2)请将统计表和扇形统计图补充完整;
(3)在统计图中“B”部分所对应的圆心角是度.
(4)若该市有120万人,估计该市态度为“A.顾客出面制止”的有万人. -
科目: 来源: 题型:
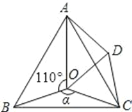
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACE=∠AEC.
(1)若CE平分∠ACD,求证:AB∥CD.
(2)若AB∥CD,求证:CE平分∠ACD.请在(1)、(2)中选择一个进行证明.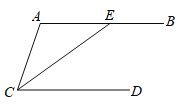
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣8,4)、(2,﹣8),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以
 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的
 ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.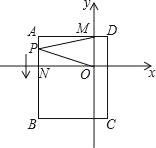
-
科目: 来源: 题型:
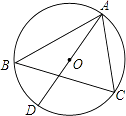
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD是⊙O直径,若∠ABC=50°,则∠CAD=度.
相关试题

