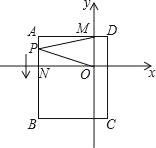
【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣8,4)、(2,﹣8),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以![]() 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的![]() ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
参考答案:
【答案】(1)B(﹣8,﹣8),D(2,4),120;(2)∠MPO=∠AMP+∠PON;∠MPO=∠AMP-∠PON;(3)存在,P点坐标为(﹣8,﹣6).
【解析】
(1)利用点A、C的坐标和长方形的性质易得B(﹣8,﹣8),D(2,4),然后根据长方形的面积公式即可计算长方形ABCD的面积;
(2)分点P在线段AN上和点P在线段NB上两种情况进行讨论即可得;
(3)由于AM=8,AP=![]() t,根据三角形面积公式可得S△AMP =t,再利用三角形AMP的面积等于长方形面积的
t,根据三角形面积公式可得S△AMP =t,再利用三角形AMP的面积等于长方形面积的![]() ,即可计算出t=20,从而可得AP=10,再根据点的坐标的表示方法即可写出点P的坐标.
,即可计算出t=20,从而可得AP=10,再根据点的坐标的表示方法即可写出点P的坐标.
(1)∵点A、C坐标分别为(﹣8,4)、(2,﹣8),
∴B(﹣8,﹣8),D(2,4),
长方形ABCD的面积=(2+8)×(4+8)=120;
(2)当点P在线段AN上时,作PQ∥AM,如图,
∵AM∥ON,∴AM∥PQ∥ON,∴∠QPM=∠AMP,∠QPO=∠PON,
∴∠QPM+∠QPO=∠AMP+∠PON,即∠MPO=∠AMP+∠PON;
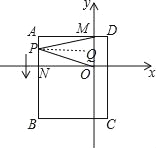
当点P在线段NB上时,作PQ∥AM,如图,
∵AM∥ON,∴AM∥PQ∥ON,∴∠QPM=∠AMP,∠QPO=∠PON,
∴∠QPM-∠QPO=∠AMP-∠PON,即∠MPO=∠AMP-∠PON;

(3)存在,
∵AM=8,AP=![]() t,∴S△AMP=
t,∴S△AMP=![]() ×8×
×8×![]() t=2t,
t=2t,
∵三角形AMP的面积等于长方形面积的![]() ,
,
∴2t=120×![]() =40,∴t=20,AP=
=40,∴t=20,AP=![]() ×20=10,
×20=10,
∵AN=4,
∴PN=6
∴P点坐标为(﹣8,﹣6).
-
科目: 来源: 题型:
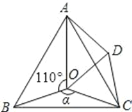
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
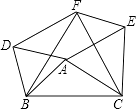
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACE=∠AEC.
(1)若CE平分∠ACD,求证:AB∥CD.
(2)若AB∥CD,求证:CE平分∠ACD.请在(1)、(2)中选择一个进行证明.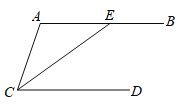
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD是⊙O直径,若∠ABC=50°,则∠CAD=度.
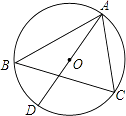
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简或求值
(1)若A=-2a2+ab-b3,B=a2-2ab+b3,求A -2B的值。
(2)先化简,再求值:5x2y-3xy2-7(x2y- xy
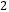 ),其中x=2,y=-1。
),其中x=2,y=-1。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
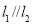 ,直线
,直线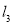 交
交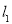 于
于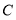 点,交
点,交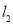 于
于 点,
点, 是线段
是线段 上的一个动点,
上的一个动点,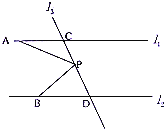
(1)若
 点在线段
点在线段 (
( 、
、 两点除外)上运动,问
两点除外)上运动,问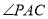 ,
,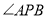 ,
,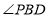 之间的关系是什么?这种关系是否变化?
之间的关系是什么?这种关系是否变化?(2)若
 点在线段
点在线段 之外时,
之外时,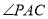 ,
,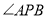 ,
,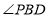 之间的关系怎样?说明理由
之间的关系怎样?说明理由
相关试题

