【题目】如图,网格的每个小正方形的边长都是1个单位长度,正方形AGFB和正方形ACDE的顶点都在网格格点上. 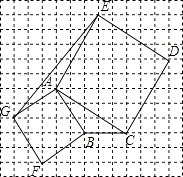
(1)建立平面直角坐标系,使点B、C的坐标分别为(0,0)和(3,0),写出点A、D、E、F、G的坐标,并指出它们所在象限.
(2)计算三角形AGF和三角形ABC的面积.
(3)作图:过点A作BC的垂线,与GE交于点K,垂足为H.请测量图中的线段KE、GK的长度(回答实际测量值)? 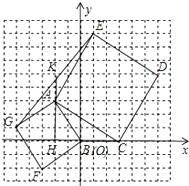
参考答案:
【答案】
(1)解:平面直角坐标系如图所示,

A(﹣2,3)在第二象限,D(6,5)在 第一象限,E(1,8)在第一象限,G(﹣5,1)在第二象限,F(﹣3,﹣2)在第三象限
(2)解:S△AGF= ![]() S正方形AGFB=
S正方形AGFB= ![]() (
( ![]() )2=6.5,
)2=6.5,
S△ABC= ![]() 33=4.5
33=4.5
(3)解:由图像可知KE=4.2,KG=5
【解析】
【考点精析】认真审题,首先需要了解三角形的面积(三角形的面积=1/2×底×高).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于点C(0,5).
(1)求该抛物线所对应的函数关系式;
(2)D是笫一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD.设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围;
②当m为何值时,S有最大值,并求这个最大值;
③直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a3a3=2a3 B. (a5)2=a7 C. (ab2)3=ab6 D. (a3)2÷(a2)3=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
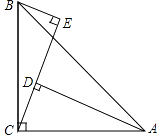
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-x)2·x3÷(-x)3;
(2)(2x-3y)·(2x-3y)4·(3y-2x)3÷(3y-2x)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α,β是方程x2+2017x+1=0的两个根,则(α2+2018α+1)(β2+2018β+1)的值_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥CD,CD⊥BC,AC平分∠BAD.
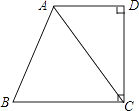
(1)求证:∠ACB=∠BAC;
(2)若∠B=80°,求∠DCA的度数.
相关试题

