【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于点C(0,5).
(1)求该抛物线所对应的函数关系式;
(2)D是笫一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD.设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围;
②当m为何值时,S有最大值,并求这个最大值;
③直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.

参考答案:
【答案】(1)抛物线的函数关系式为y=﹣x2+4x+5;
(2)①S关于m的函数关系式为s=﹣![]() m2+
m2+![]() m (0<m<5);
m (0<m<5);
②当m=![]() 时,S有最大值,S最大值=
时,S有最大值,S最大值=![]() ;
;
③直线BC能把△BDF分成面积之比为2:3的两部分,点D的坐标为(![]() )或(
)或(![]() )
)
【解析】(1)由抛物线与x轴的两个交点坐标可设抛物线的解析式y=a(x+1)(x-5),将点C(0,3)代入抛物线解析式中即可得出关于a一元一次方程,解方程即可求出a的值,从而得出抛物线的解析式;
(2)设直线BC的函数解析式为y=kx+b,结合点B、点C的坐标,利用待定系数法求出直线BC的函数解析式,再由点横坐标为m得出点D、点E的坐标,结合两点间的距离公式以及三角形的面积公式,即可得出结论; 由 的结论,利用配方法将S关于m的函数关系式进行变形,从而得出结论;
结合图象可知△BDE和△BFE是等高的,由此得出它们的面积比=DE:EF,分两种情况考虑,根据两点间的距离公式即可得出关于m的分式方程,解方程即可得出m的值,将其代入到点D的坐标中即可得出结论.
(1)∵抛物线经过A(﹣1,0),B(5,0),C(0,5),
∴设y=a(x+1)(x﹣5),
∴5=a(0+1)(0﹣5),
解得a=﹣1,
∴抛物线的函数关系式为y=﹣(x+1)(x﹣5),
即y=﹣x2+4x+5;
(2)①设直线BC的函数关系式为y=kx+b,则
![]() 解得
解得![]() ,
,
∴y=﹣x+5,
设D(m,﹣m2+4m+5),E(m,﹣m+5),
∴DE=﹣m2+4m+5+m﹣5=﹣m2+5m
∴s=![]() (﹣m2+5m)=﹣
(﹣m2+5m)=﹣![]() m2+
m2+![]() m (0<m<5);
m (0<m<5);
②s=﹣![]() m2+
m2+![]() m=
m=![]() ,
,
∵![]() ,
,
∴当m=![]() 时,S有最大值,S最大值=
时,S有最大值,S最大值=![]() ;
;
③∵△BDE和△BFE是等高的,
∴它们的面积比=DE:EF,
(ⅰ)当DE:EF=2:3时,
即![]() ,
,
解得:![]() (舍),
(舍),
此时,D(![]() );
);
(ⅱ)当DE:EF=3:2时,
即![]() ,
,
解得:![]() (舍),
(舍),
此时,D(![]() ).
).
综上所述,点D的坐标为(![]() )或(
)或(![]() ).
).
“点睛”本题属于二次函数综合题,主要考查了二次函数的性质、待定系数法求函数解析式、两点间的公式以及三角形的面积公式的综合应用,解题的关键是运用待定系数法求解析式;找出直线BC的函数解析式;运用配方法解决问题.解题时注意分类讨论的思想的运用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为
 ,求BC的长.
,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:tan45°=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列数为4, 7, 10……那么第n个数是__________(用含n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a3a3=2a3 B. (a5)2=a7 C. (ab2)3=ab6 D. (a3)2÷(a2)3=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
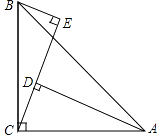
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格的每个小正方形的边长都是1个单位长度,正方形AGFB和正方形ACDE的顶点都在网格格点上.
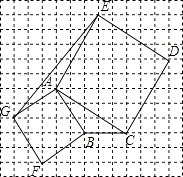
(1)建立平面直角坐标系,使点B、C的坐标分别为(0,0)和(3,0),写出点A、D、E、F、G的坐标,并指出它们所在象限.
(2)计算三角形AGF和三角形ABC的面积.
(3)作图:过点A作BC的垂线,与GE交于点K,垂足为H.请测量图中的线段KE、GK的长度(回答实际测量值)?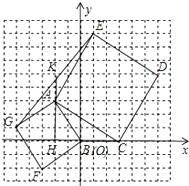
相关试题

