【题目】已知:如图,在ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=![]() BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
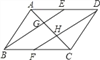
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】分析:(1)根据BF∥DE,BF=DE可证BEDF为平行四边形;(2)根据平行线等分线段定理判断;(3)根据△AGE∽△CGB可得;
(4)由(3)可得△ABG的面积=△AGE面积×2.
详解:(1)∵ABCD,∴AD=BC,AD∥BC.
E、F分别是边AD、BC的中点,
∴BF∥DE,BF=DE.
∴BEDF为平行四边形,BE=DF.故正确;
(2)根据平行线等分线段定理可得AG=GH=HC.故正确;
(3)∵AD∥BC,AE=![]() AD=
AD=![]() BC,
BC,
∴△AGE∽△CGB,AE:BC=EG:BG=1:2,
∴EG=![]() BG.故正确.
BG.故正确.
(4)∵BG=2EG,∴△ABG的面积=△AGE面积×2,
∴S△ABE=3S△AGE.故正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的高线,BD=CD,点E是AD上一点,BE=BC,将△ABE沿BE所在直线折叠,点A落在点A′位置上,连接AA',BA′,EA′与AC相交于点H,BA′与AC相交于点F.小夏依据上述条件,写出下列四个结论:①∠EBC=60°;②∠BFC=60°;③∠EA′A=60°;④∠A′HA=60°.以上结论中,正确的是( )

A.①B.③④C.①②③D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,将
,将 绕点
绕点 顺时针旋转得到
顺时针旋转得到 .
. 如图
如图 ,
, ________°;
________°; 连接
连接 交直线
交直线 于点
于点 ,直线
,直线 交
交 于点
于点 .
.①如图
 所示,试说明
所示,试说明 ;
;②设
 ,旋转的角度
,旋转的角度 ,当
,当 、
、 满足什么关系时,
满足什么关系时, 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,在平面内,如果一个图形绕着一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转的这个角称为这个图形的一个旋转角.例如,正方形绕着它的对角线的交点旋转
 后能与自身重合所以正方形是旋转对称图形,它有一个旋转角为
后能与自身重合所以正方形是旋转对称图形,它有一个旋转角为 .
. 判断下列说法是否正确(在相应横线里填上“对”或“错”)
判断下列说法是否正确(在相应横线里填上“对”或“错”)①正五边形是旋转对称图形,它有一个旋转角为
 .________
.________②长方形是旋转对称图形,它有一个旋转角为
 .________
.________ 填空:下列图形中时旋转对称图形,且有一个旋转角为
填空:下列图形中时旋转对称图形,且有一个旋转角为 的是________.(写出所有正确结论的序号)
的是________.(写出所有正确结论的序号)①正三角形②正方形③正六边形④正八边形
 写出两个多边形,它们都是旋转对称图形,都有一个旋转角为
写出两个多边形,它们都是旋转对称图形,都有一个旋转角为 ,其中一个是轴对称图形,但不是中心对称图形;另一个既是轴对称图形,又是中心对称图形.
,其中一个是轴对称图形,但不是中心对称图形;另一个既是轴对称图形,又是中心对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
例如:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
…
请你猜想(a+b)9的展开式中所有系数的和是( )

A.2018B.512C.128D.64
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F,D是BC边上的中点,连结AD.

(1)若∠BAD=55°,求∠C的度数;
(2)猜想FB与FE的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是四边形
是四边形 的对角线
的对角线 上一点,且
上一点,且 .从图中找出
.从图中找出 对相似三角形,它们是________.
对相似三角形,它们是________.
相关试题

