【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

参考答案:
【答案】见解析
【解析】试题分析:(1)根据题中条件可证明△AOB≌△AOD,得到OD=OB,可证点D在△ABE的外接圆上;
(2)根据∠C=90°,可得∠CED+∠CDE=90°;利用∠ODE=∠DEC,可知∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°,即CD与△ABE的外接圆相切.
试题解析:证明:(1)∵∠B=90°,∴AE是△ABE外接圆的直径.
取AE的中点O,则O为圆心,连接OB、OD.
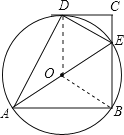
在△AOB和△AOD中,∵AB=AD,∠BAC=∠DAO,AO=AO,∴△AOB≌△AOD.∴OD=OB,∴点D在△ABE的外接圆上.
(2)直线CD与△ABE的外接圆相切.
理由:∵AB∥CD,∠B=90°.∴∠C=90°,∴∠CED+∠CDE=90°.
又∵OE=OD,∴∠ODE=∠OED.
又∠AED=∠CED,∴∠ODE=∠DEC,∴∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°,∴CD与△ABE的外接圆相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD中,AE⊥BD于点E,CF⊥BD于点F.
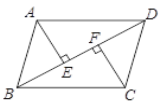
(1)求证:BF=DE;
(2)如果∠ABC=75°, ∠DBC=30°,BC=2,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).

(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题:
在首届“一带一路”国际合作高峰论坛举办之后,某工厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知3件甲种商品与5件乙种商品的销售收入相同,2件甲种商品比3件乙种商品的销售收入多200元. 问甲、乙两种商品的销售单价分别是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,AD=10.
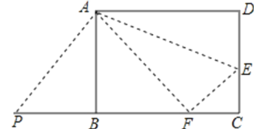
(1)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.求DE的长;
(2)点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长;
(3)M是AD上的动点,在DC上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,请直接写出线段CT长度的最大值与最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
1月
2月
3月
4月
5月
甲
9
9
8
7
5
乙
10
9
6
8
8
丙
11
10
5
5
9
(1)根据上表中的数据,将下表补充完整:
平均数
(万元)
众数
(万元)
中位数
(万元)
甲
7. 6
8
乙
8
8
丙
8
5
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
相关试题

