搜索
【题目】列方程组解应用题：
在首届“一带一路”国际合作高峰论坛举办之后，某工厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区，已知3件甲种商品与5件乙种商品的销售收入相同，2件甲种商品比3件乙种商品的销售收入多200元. 问甲、乙两种商品的销售单价分别是多少元？
参考答案：
【答案】甲种商品的销售单价是1000元，乙种商品的销售单价是600元.
【解析】
设甲种商品的销售单价为x元/件，乙种商品的销售单价为y元/件，根据“3件甲种商品与5件乙种商品的销售收入相同，2件甲种商品比3件乙种商品的销售收入多200元”，即可得出关于x、y的二元一次方程组，解之即可得出结论．
设甲、乙两种商品的销售单价分别是
元、
元，
根据题意，得
，
解这个方程组，得
，
答：甲种商品的销售单价是1000元，乙种商品的销售单价是600元.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB的顶点均在格点上，点O为原点，点A、B的坐标分别是A（3，2）、B（1，3）．
（1）将△AOB向下平移3个单位后得到△A1O1B1，则点B1的坐标为 ；
（2）将△AOB绕点O逆时针旋转90°后得到△A2OB2，请在图中作出△A2OB2，并求出这时点A2的坐标为 ；
（3）在（2）中的旋转过程中，线段OA扫过的图形的面积 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．
（1）求证：四边形AECD是菱形；
（2）若点E是AB的中点，试判断△ABC的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB∥CD，∠B=90°，AB=AD，∠BAD的平分线交BC于E，连接DE．
（1）说明点D在△ABE的外接圆上；
（2）若∠AED=∠CED，试判断直线CD与△ABE外接圆的位置关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB=8，AD=10．
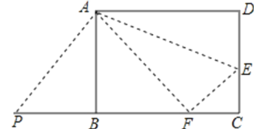
（1）E是CD上的点，将△ADE沿折痕AE折叠，使点D落在BC边上点F处．求DE的长；
（2）点P是线段CB延长线上的点，连接PA，若△PAF是等腰三角形，求PB的长；
（3）M是AD上的动点，在DC上存在点N，使△MDN沿折痕MN折叠，点D落在BC边上点T处，请直接写出线段CT长度的最大值与最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位：万元)如下表：
1月
2月
3月
4月
5月
甲
9
9
8
7
5
乙
10
9
6
8
8
丙
11
10
5
5
9
(1)根据上表中的数据，将下表补充完整：
平均数
(万元)
众数
(万元)
中位数
(万元)
甲
7. 6
8
乙
8
8
丙
8
5
(2)甲、乙、丙三名业务员都说自己的销售业绩好，你赞同谁的说法？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于正数
，用符号
表示的整数部分，例如：
，
，
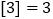．点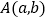
在第一象限内，以A为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直. 其中垂直于
轴的边长为
，垂直于轴的边长为
，那么，把这个矩形覆盖的区域叫做点A的矩形域．例如：点
的矩形域是一个以为对角线交点，长为3，宽为2的矩形所覆盖的区域，如图1所示，它的面积是6．
图1 图2
根据上面的定义，回答下列问题：
（1）在图2所示的坐标系中画出点 的矩形域，该矩形域的面积是 ；
（2）点
的矩形域重叠部分面积为1，求的值； （3）已知点
在直线
上， 且点B的矩形域的面积
满足
，那么
的取值范围是 ．（直接写出结果）
相关试题
