【题目】 (本小题8分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.

(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
参考答案:
【答案】(1)详见解析;(2)y=x2-![]() x+1;(3)AE的长为2-
x+1;(3)AE的长为2-![]() 或
或![]() .
.
【解析】
试题分析:(1)根据等腰直角三角形的性质及三角形内角与外角的关系,易证△ABD∽△DCE;(2)由△ABD∽△DCE,对应边成比例及等腰直角三角形的性质可求出y与x的函数关系式;(3)当△ADE是等腰三角形时,因为三角形的腰和底不明确,所以应分AD=DE,AE=DE,AD=AE三种情况讨论求出满足题意的AE的长即可.
试题解析:(1)证明:∵∠BAC=90°,AB=AC,
∴∠B=∠C=∠ADE=45°,
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE
∴∠BAD=∠CDE
∴△ABD∽△DCE;
由(1)得△ABD∽△DCE,
∴![]()
∵∠BAC=90°,AB=AC=1,
∴BC=![]() ,DC=
,DC=![]() -x,EC=1-y,
-x,EC=1-y,
∴![]()
∴y=x2-![]() x+1
x+1
(3)当AD=DE时,△ABD≌△CDE,
∴BD=CE,
∴x=1-y,即 ![]() x-x2=x,∵x≠0,
x-x2=x,∵x≠0,
∴等式左右两边同时除以x得:x=![]() -1
-1
∴AE=1-x=2-![]() ,
,
当AE=DE时,DE⊥AC,此时D是BC中点,E也是AC的中点,
所以,AE=![]() ;
;
当AD=AE时,∠DAE=90°,D与B重合,不合题意;
综上,在AC上存在点E,使△ADE是等腰三角形,
AE的长为2-![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形
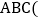 记作
记作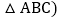 在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,先将
在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,先将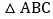 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到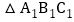 .
.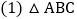 三个顶点的坐标分别是:
三个顶点的坐标分别是: ______
______ ,
, ______
______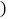 ,
,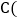 ______
______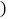 ,
,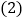 在图中画出
在图中画出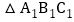 ;
;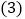 平移后
平移后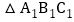 的三个顶点坐标分别为:
的三个顶点坐标分别为: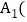 ______
______ 、
、 ______
______ 、
、 ______
______ ;
;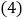 若y轴有一点P,使
若y轴有一点P,使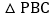 与
与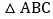 面积相等,则P点的坐标为______.
面积相等,则P点的坐标为______.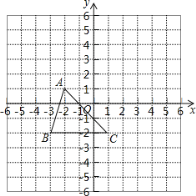
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了奖励学习进步的同学,某班准备购买甲、乙、丙三种不同的笔记本作为奖品,其单价分别为2元、3元、4元,购买这些笔记本需要花60元;经过协商,每种笔记本单价下降0.5元,只花了49元,那么以下哪个结论是正确的( )
A. 乙种笔记本比甲种笔记本少4本
B. 甲种笔记本比丙种笔记本多6本
C. 乙种笔记本比丙种笔记本多8本
D. 甲种笔记本与乙种笔记本共12本
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校综合实践活动小组的同学为了解七年级学生上学期参加综合实践活动的情况,随机抽样调查了学校部分七年级学生一个学期参加综合实践活动的情况,并用得到的数据绘制了下面两幅不完整的统计图.

根据统计图中的信息解决问题:
(1)扇形统计图中的a= ,并把条形统计图补充完整;
(2)对于“综合实践活动为6天”的扇形,对应的圆心角为 度;
(3)如果全市七年级共有12000名学生,通过计算说明“综合实践活动不超过4天”的有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:在等腰直角三角形ABC中,
 , 直线
, 直线 过点
过点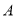 且
且 ,过点
,过点 为一锐角顶点作
为一锐角顶点作 ,且点
,且点 在直线
在直线 上(不与点
上(不与点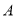 重合),如图1,
重合),如图1,  与
与 交于点
交于点 ,试判断
,试判断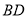 与
与 的数量关系,并说明理由.探究展示:小星同学展示出如下正确的解法:
的数量关系,并说明理由.探究展示:小星同学展示出如下正确的解法:解:
 ,证明如下:
,证明如下:过点
 作
作 ,交
,交 于点
于点
则
 为等腰直角三角形
为等腰直角三角形

 (依据
(依据 )
)在
 与
与 中
中

 (依据
(依据 )
)
(1)反思交流:上述证明过程中的“依据
 ”和“依据
”和“依据 ”分别是指:
”分别是指:依据
 :
: 依据
 :
: 拓展延伸:(2)在图2中,
 与
与 延长线交于点
延长线交于点 ,试判断
,试判断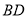 与
与 的数量关系,并写出证明过程
的数量关系,并写出证明过程(3)在图3中,
 与
与 延长线交于点
延长线交于点 ,试判断
,试判断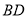 与
与 的数量关系,并写出证明过程.
的数量关系,并写出证明过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形
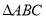 中,
中,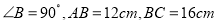 ,点
,点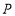 从
从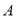 开始沿
开始沿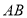 边向点
边向点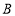 以
以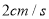 的速度移动,点
的速度移动,点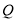 从点
从点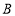 开始沿
开始沿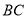 边向点
边向点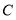 以
以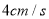 的速度移动.
的速度移动.  分别从
分别从 同时出发,当一个动点到达终点则另一动点也随之停止运动,
同时出发,当一个动点到达终点则另一动点也随之停止运动,(1)求
 为何值时,
为何值时,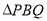 为等腰三角形?
为等腰三角形?(2)是否存在某一时刻
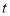 ,使点
,使点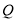 在线段
在线段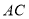 的垂直平分线上?
的垂直平分线上?(3)点
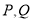 在运动的过程中,是否存在某时刻
在运动的过程中,是否存在某时刻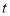 , 直线
, 直线 把
把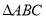 的周长分为
的周长分为 两部分?若存在,求出
两部分?若存在,求出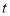 ,若不存在,请说明理由.
,若不存在,请说明理由.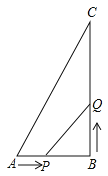
相关试题

