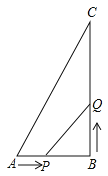
【题目】如图,在直角三角形![]() 中,
中,![]() ,点
,点![]() 从
从![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.
的速度移动. ![]() 分别从
分别从![]() 同时出发,当一个动点到达终点则另一动点也随之停止运动,
同时出发,当一个动点到达终点则另一动点也随之停止运动,
(1)求![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(2)是否存在某一时刻![]() ,使点
,使点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(3)点![]() 在运动的过程中,是否存在某时刻
在运动的过程中,是否存在某时刻![]() , 直线
, 直线![]() 把
把![]() 的周长分为
的周长分为![]() 两部分?若存在,求出
两部分?若存在,求出![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
参考答案:
【答案】(1)2;(2)存在,![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)根据题意用t表示出BP、BQ,根据等腰三角形的概念列方程,解方程得到答案;
(2)根据线段垂直平分线的性质得到QA=QC,列方程,解方程即可;
(3)分AC+AP+CQ=2(BP+BQ)、2(AC+AP+CQ)=BP+BQ两种情况计算,得到答案.
![]() 由题意得,
由题意得,![]()
则![]()
当![]() 为等腰三角形时,
为等腰三角形时,
只有![]()
![]()
解得,![]()
![]() 当点
当点![]() 在线段
在线段![]() 的垂直平分线上时,连接QA,
的垂直平分线上时,连接QA,

![]()
设![]()
则![]()
解得,![]() 即
即![]()
![]() (秒)
(秒)
![]() 在
在![]() 中,
中,
![]()
当直线![]() 把
把![]() 的周长分为
的周长分为![]() 两部分时,
两部分时,
①当![]() 时,
时,
![]()
解得,![]()
②当![]() 时,
时,
![]()
解得,![]()
![]() 当
当![]() 或
或![]() 时,直线
时,直线![]() 把
把![]() 的周长分为
的周长分为![]() 两部分.
两部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (本小题8分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.

(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校综合实践活动小组的同学为了解七年级学生上学期参加综合实践活动的情况,随机抽样调查了学校部分七年级学生一个学期参加综合实践活动的情况,并用得到的数据绘制了下面两幅不完整的统计图.

根据统计图中的信息解决问题:
(1)扇形统计图中的a= ,并把条形统计图补充完整;
(2)对于“综合实践活动为6天”的扇形,对应的圆心角为 度;
(3)如果全市七年级共有12000名学生,通过计算说明“综合实践活动不超过4天”的有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:在等腰直角三角形ABC中,
 , 直线
, 直线 过点
过点 且
且 ,过点
,过点 为一锐角顶点作
为一锐角顶点作 ,且点
,且点 在直线
在直线 上(不与点
上(不与点 重合),如图1,
重合),如图1,  与
与 交于点
交于点 ,试判断
,试判断 与
与 的数量关系,并说明理由.探究展示:小星同学展示出如下正确的解法:
的数量关系,并说明理由.探究展示:小星同学展示出如下正确的解法:解:
 ,证明如下:
,证明如下:过点
 作
作 ,交
,交 于点
于点
则
 为等腰直角三角形
为等腰直角三角形

 (依据
(依据 )
)在
 与
与 中
中

 (依据
(依据 )
)
(1)反思交流:上述证明过程中的“依据
 ”和“依据
”和“依据 ”分别是指:
”分别是指:依据
 :
: 依据
 :
: 拓展延伸:(2)在图2中,
 与
与 延长线交于点
延长线交于点 ,试判断
,试判断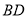 与
与 的数量关系,并写出证明过程
的数量关系,并写出证明过程(3)在图3中,
 与
与 延长线交于点
延长线交于点 ,试判断
,试判断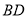 与
与 的数量关系,并写出证明过程.
的数量关系,并写出证明过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两站的路程是312km,一列列车从甲站开往乙站,设列车的平均速度为xkm/h,所需时间为yh.
(1)试写出y关于x的函数关系式;
(2)2006年全国铁路第六次大提速前,这列列车从甲站到乙站需要4h,列车提速后,速度提高了26km/h,问提速后从甲站到乙站需要几个小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在新罗区中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要5.5万元,购买2台电脑和1台电子白板需要5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过50万元,则最多能购买电子白板多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,∠A=∠B=70°.请按如下要求操作并解答:

(1)在图中,过点A画直线MP∥BC,过点C画直线NP⊥AB,直线MP与NP交于点P,求∠APC的度数;
(2)在(1)的前提下,直线PM上存在点D,且∠ABD=∠ADB,求直线BD与直线PN相交所形成的锐角的度数.
相关试题

