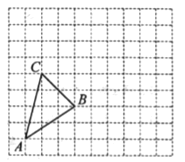
【题目】如图,在△![]() 中,∠ACB=90°,∠ABC与∠BAC的角平分线相交于点P,连接CP,过点P作DE⊥CP分别交AC、BC于点D、E,
中,∠ACB=90°,∠ABC与∠BAC的角平分线相交于点P,连接CP,过点P作DE⊥CP分别交AC、BC于点D、E,

(1)若∠BAC=40°,求∠APB与∠ADP度数;
(2)探究:通过(1)的计算,小明猜测∠APB=∠ADP,请你说明小明猜测的正确性(要求写出过程).
参考答案:
【答案】(1)![]() ,
,![]() ;(2)正确,理由见解析.
;(2)正确,理由见解析.
【解析】
(1)根据三角形的三条角平分线交于一点可知CP平分∠BCA,可得∠PCD=45°,从而由三角形外角性质可求∠ADP=135°,再∠BAC=40°,可求∠BAC度数,根据角平分线的定义求出![]() ,然后利用三角形的内角和定理列式计算即可得解.
,然后利用三角形的内角和定理列式计算即可得解.
(2)同理(1)直接可得![]() .由角平分线可求
.由角平分线可求![]() ,进而可得
,进而可得![]() ,由此得出结论.
,由此得出结论.
解:(1)![]() ,
,![]() ,∠BAC=40°,
,∠BAC=40°,
![]() .
.
![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,
![]() ,
,![]() .
.
![]()
![]() ,
,
![]() .
.
![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,
∴CP是∠ACB的角平分线,
∴∠PCD=![]() ,
,
∵DE⊥CP,
∴![]() ,
,
∴![]() .
.
终上所述:![]() ,
,![]() .
.
∴![]() ∠ADP=
∠ADP=
(2)小明猜测是正确的,理由如下:
![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,
∴CP是∠ACB的角平分线,
∴∠PCD=![]() ,
,
∵DE⊥CP,
∴![]() ,
,
∴![]() .
.
![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,
![]() ,
,![]() .
.
∵![]() ,
,
∴![]()
![]()
![]() ,
,
![]() .
.
故∠APB=∠ADP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块长为
 米,宽为
米,宽为 米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为
米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为 米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
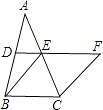
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校有一块长为(5a+b)米,宽为(3a+b)米的长方形空地,中间是边长(a﹣b)米的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,求证:PQ=
 BP.
BP.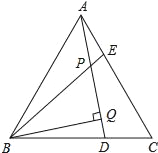
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市火车站北广场将于2016年底投入使用,计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600 棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排13人同时种植这两种花木,每人每天能种植A花木60棵或B花木40 棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
相关试题

