搜索
【题目】如图，有一块长为
米，宽为
米的长方形空地，计划修筑东西、南北走向的两条道路，其余进行绿化（阴影部分），已知道路宽为
米，东西走向的道路与空地北边界相距1米，则绿化的面积是多少平方米？并求出当a＝3，b＝2时的绿化面积．
参考答案：
【答案】
平方米；40平方米．
【解析】
（1）根据平移的原理，四块绿化面积可拼成一个长方形，其边长为原边长减去再减去道路宽为
米，由此即可求绿化的面积的代数式；然后利用多项式乘多项式法则计算，去括号合并得到最简结果，将与
的值代入计算即可求出值．
解：根据题意得：
（平方米）．
则绿化的面积是平方米；
当
，
时，原式
（平方米）．
故当a＝3，b＝2时，绿化面积为40平方米．
答：绿化的面积是平方米；当a＝3，b＝2时，绿化面积为40平方米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，AB=5cm，AC⊥AB，BD⊥AB，AC=BD=4cm，点P在线段AB上以1cm/s的速度由A向B运动，同时，点Q在线段BD上由点B向点D运动，它们运动时间为t（s）．
（1）若点Q的运动速度与点P速度相等，当t=1，△ACP与△BPQ是否全等？请说明理由，并推导出此时线段PC和线段PQ的位置关系；
（2）如图2，将图1中的“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA=α°”，其他条件不变，设点Q的运动速度为xcm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x，t的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD．当△AOD是等腰三角形时，求α的角度为______
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示的正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的顶点都在正方形网格的格点（网格线的交点）上．
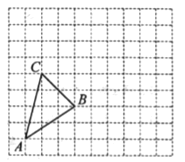
（1）画出△ABC先向右平移5个单位长度，再向上平移2个单位长度所得的△A1B1C1；
（2）画出△ABC的中线AD；
（3）画出△ABC的高CE所在直线，标出垂足E：
（4）在（1）的条件下，线段AA1和CC1的关系是
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，D，E分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．
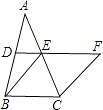
（1）求证：四边形BCFE是菱形；
（2）若CE=4，∠BCF=120°，求菱形BCFE的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△
中，∠ACB＝90°，∠ABC与∠BAC的角平分线相交于点P，连接CP，过点P作DE⊥CP分别交AC、BC于点D、E，
(1)若∠BAC＝40°，求∠APB与∠ADP度数；
(2)探究：通过（1）的计算，小明猜测∠APB＝∠ADP，请你说明小明猜测的正确性（要求写出过程）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某校有一块长为（5a+b）米，宽为（3a+b）米的长方形空地，中间是边长（a﹣b）米的正方形草坪，其余为活动场地，学校计划将活动场地（阴影部分）进行硬化．
（1）用含a，b的代数式表示需要硬化的面积并化简；
（2）当a=5，b=2时，求需要硬化的面积．
相关试题
