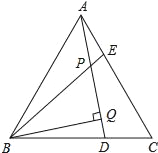
【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,求证:PQ=![]() BP.
BP.
参考答案:
【答案】证明见解析.
【解析】
由△ABC是等边三角形可得AB=AC,∠BAE=∠ACD=60°,结合AE=CD可得△ABE≌△CAD,由此可得∠ABE=∠CAD,结合∠BPQ=∠ABE+∠BAP可得∠BPQ=∠BAP+∠CAD=∠BAC=60°,再结合BQ⊥AD即可得到∠BQP=90°,∠PBQ=30°,由此即可得到PQ=![]() BP.
BP.
∵△ABC为等边三角形,
∴∠C=∠BAC=60°,AB=AC,
又∵AE=CD,
∴△ABE≌△CAD(SAS),
∴∠BAE=∠CAD,
∵∠BPQ=∠ABE+∠BAP,
∴∠BPQ=∠BAP+∠CAD=∠BAC=60°,
又∵BQ⊥AD,
∴∠BQP=90°,∠PBQ=30°,
∴PQ=![]() BP.
BP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程
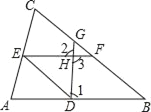
如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(________),
∴∠1+∠3=180°
∴______∥______(________)
∴∠B=______(________)
∵∠B=∠DEF(已知)
∴∠DEF=______(等量代换)
∴DE∥BC(________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=
 ,BG=
,BG= ,且
,且 、
、 满足下列关系:
满足下列关系: ,
, ,则GH= .
,则GH= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足x12+x22=3x1x2 , 求实数p的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①所示,试说明OB∥AC;
(2)如图②,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可);
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(4)在(3)的条件下,在平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA的度数等于________(在横线上填上答案即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


相关试题

