搜索
【题目】如图，在△ABC中，∠C=90°，点E是AC上的点，且∠1=∠2，DE垂直平分AB，垂足是D，如果EC=3 cm，那么AE等于（ ）
A.3 cm
B.
cm
C.6 cm
D.
cm
参考答案：
【答案】C
【解析】根据DE为AB的中垂线可得：AE=BE，∠A=∠2，根据∠1=∠2可根据角平分线的性质可得：DE=CE=3cm，根据∠C=90°可得：∠1+∠2+∠A=90°，则∠1=∠2=∠A=30°，根据Rt△ADE的勾股定理可得：AE=2DE=6cm．
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角，以及对线段垂直平分线的性质的理解，了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．如果一条直线与果圆只有一个交点，则这条直线叫做果圆的切线．已知A、B、C、D四点为果圆与坐标轴的交点，E为半圆的圆心，抛物线的解析式为y=x2﹣2x﹣3，AC为半圆的直径．
（1）分别求出A、B、C、D四点的坐标；
（2）求经过点D的果圆的切线DF的解析式；
（3）若经过点B的果圆的切线与x轴交于点M，求△OBM的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，AB＝4，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG＝1，则AE的长为（ ）
A.
B.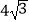
C.4
D.8 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠B＝∠D＝90°，∠C＝60°，AD＝1，BC＝2，求AB、CD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】李明同时掷甲、乙两枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y，这样就确定点P的一个坐标（
， 
），那么点P落在双曲线 
上的概率为（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为深化课程改革，某校为学生开设了形式多样的社团课程，为了解部分社团课程在学生中最受欢迎的程度，学校随机抽取七年级
名学生进行调查，从
：文学鉴赏，
：科学探究，
：文史天地，
：趣味数学四门课程中选出你喜欢的课程（被调查的每名学生必选且只能选择一门课程），并将调查结果制成如下两幅不完整的统计图：
（1）
_________，
_________；（2）扇形统计图中，“
”所对应的扇形的圆心角度数是________度；（3）请根据以上信息直接在答题卡中补全条形统计图.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE，DF，EF．在此运动变化的过程中，有下列结论：
①△DFE是等腰直角三角形；
②四边形CEDF不可能为正方形；
③四边形CEDF的面积随点E位置的改变而发生变化；
④点C到线段EF的最大距离为
．
其中正确结论的个数是（ ）
A.1个
B.2个
C.3个
D.4个
相关试题
