【题目】如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AD=1,BC=2,求AB、CD的长.

参考答案:
【答案】AB=2![]() -2,CD=4-
-2,CD=4-![]() .
.
【解析】
此题为几何题,看题目只是一个四边形,要求两条未知边,那肯定要添辅助线.过点D作DH⊥BA延长线于H,作DM⊥BC于M.构建矩形HBMD.利用矩形的性质和解直角三角形来求AB、CD的长度.
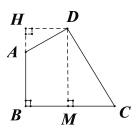
如图,过点D作DH⊥BA延长线于H,作DM⊥BC于点M.
∵∠B=90°,
∴四边形HBMD是矩形.
∴HD=BM,BH=MD,∠ABM=∠ADC=90°,
又∵∠C=60°,
∴∠ADH=∠MDC=30°,
∴在Rt△AHD中,AD=1,∠ADH=30°,则AH=![]() AD=
AD=![]() ,DH=
,DH=![]() .
.
∴MC=BC-BM=BC-DH=2-![]() =
=![]() .
.
∴在Rt△CMD中,CD=2MC=4-![]() ,DM=
,DM=![]() CD=
CD=![]() .
.
∴AB=BH-AH=DM-AH=![]() -
-![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,解决下列问题:
(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.
(2)如图②,若∠ABP=
 ∠ABE,∠CDP=
∠ABE,∠CDP= ∠CDE,试写出∠P与∠E的数量关系并说明理由.
∠CDE,试写出∠P与∠E的数量关系并说明理由.(3)如图③,若∠ABP=
 ∠ABE,∠CDP=
∠ABE,∠CDP= ∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).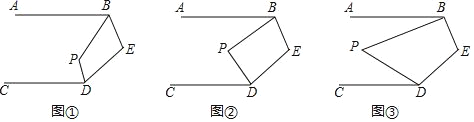
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.

(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )

A.
B.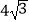
C.4
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3 cm,那么AE等于( )

A.3 cm
B. cm
cm
C.6 cm
D. cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】李明同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y,这样就确定点P的一个坐标(
 ,
,  ),那么点P落在双曲线
),那么点P落在双曲线  上的概率为( )
上的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为深化课程改革,某校为学生开设了形式多样的社团课程,为了解部分社团课程在学生中最受欢迎的程度,学校随机抽取七年级
 名学生进行调查,从
名学生进行调查,从 :文学鉴赏,
:文学鉴赏, :科学探究,
:科学探究, :文史天地,
:文史天地, :趣味数学四门课程中选出你喜欢的课程(被调查的每名学生必选且只能选择一门课程),并将调查结果制成如下两幅不完整的统计图:
:趣味数学四门课程中选出你喜欢的课程(被调查的每名学生必选且只能选择一门课程),并将调查结果制成如下两幅不完整的统计图:
(1)
 _________,
_________, _________;
_________;(2)扇形统计图中,“
 ”所对应的扇形的圆心角度数是________度;
”所对应的扇形的圆心角度数是________度;(3)请根据以上信息直接在答题卡中补全条形统计图.
相关试题

