【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒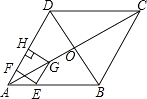
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为;当OO′⊥AD时,t的值为 .
参考答案:
【答案】
(1)
解:由题意知:AE=2t,0≤t≤4,
∵∠BAD=60°,∠AFE=90°,
∴sin∠BAD= ![]() ,
,
∴EF= ![]() t
t
(2)
解:∵AE=2t,∠AEF=30°,
∴AF=t,
当H与D重合时,
此时FH=8﹣t,
∴GE=8﹣t,
∵EG∥AD,
∴∠EGA=30°,
∵四边形ABCD是菱形,
∴∠BAC=30°,
∴∠BAC=∠EGA=30°,
∴AE=EG,
∴2t=8﹣t,
∴t= ![]()
(3)
解:当0<t≤ ![]() 时,
时,
此时矩形EFHG与菱形ABCD重叠部分图形为矩形EFHG,
∴由(2)可知:AE=EG=2t,
∴S=EFEG= ![]() t2t=2
t2t=2 ![]() t2,
t2,
当 ![]() <t≤4时,如图1,
<t≤4时,如图1,
设CD与HG交于点I,
此时矩形EFHG与菱形ABCD重叠部分图形为五边形FEGID,
∵AE=2t,
∴AF=t,EF= ![]() t,
t,
∴DF=8﹣t,
∵AE=EG=FH=2t,
∴DH=2t﹣(8﹣t)=3t﹣8,
∵∠HDI=∠BAD=60°,
∴tan∠HDI= ![]() ,
,
∴HI= ![]() DH,
DH,
∴S=EFEG﹣ ![]() DHHI=2
DHHI=2 ![]() t2﹣
t2﹣ ![]() (3t﹣8)2=﹣
(3t﹣8)2=﹣ ![]() t2+24
t2+24 ![]() t﹣32
t﹣32 ![]()

(4)4;3
【解析】解:(4)当OO′∥AD时,如图2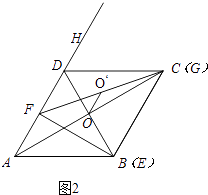
此时点E与B重合,
∴t=4;
当OO′⊥AD时,如图3,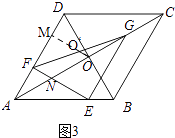
过点O作OM⊥AD于点M,EF与OA相交于点N,
由(2)可知:AF=t,AE=EG=2t,
∴FN= ![]() t,
t,
∵O′是矩形EFHG的对角线的交点,
∴FM= ![]() EG=t,
EG=t,
∵O′O⊥AD,O′是FG的中点,
∴O′O是△FNG的中位线,
∴O′O= ![]() FN=
FN= ![]() t,
t,
∵AB=8,
∴由勾股定理可求得:OA=4 ![]()
∴OM=2 ![]() ,
,
∴O′M=2 ![]() ﹣
﹣ ![]() t,
t,
∵FE= ![]() t,EG=2t,
t,EG=2t,
∴由勾股定理可求得:FG2=7t2 ,
∴由矩形的性质可知:O′F2= ![]() FG2 ,
FG2 ,
∵由勾股定理可知:O′F2=O′M2+FM2 ,
∴ ![]() t2=(2
t2=(2 ![]() ﹣
﹣ ![]() t)2+t2 ,
t)2+t2 ,
∴t=3或t=﹣6(舍去).
所以答案是:t=4;t=3.
【考点精析】利用菱形的性质对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
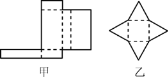
查看答案和解析>>【题目】观察图,回答下列问题:
(1)甲、乙两图分别能折成什么几何体?简述它们的特征;
(2)设几何体的面数为F,顶点数为V,棱数为E,请计算(1)中两个几何体的F+V-E的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它表示甲乙两人从同一个地点出发后的情况.根据图像判断,下列说法错误的是()

A. 甲是 8 点出发的
B. 乙是 9 点出发的,到 10 点时,他大约走了 10 千米
C. 到 10 点为止,乙的速度快
D. 两人在 12 点再次相遇
-
科目: 来源: 题型:
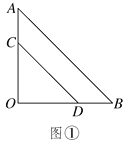
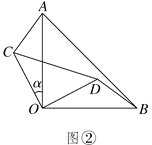
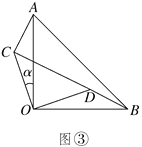
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD,BE分别是△ABC的中线和角平分线,AD⊥BE于点G,AD=BE=6,求AC的长.

-
科目: 来源: 题型:
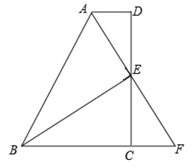
查看答案和解析>>【题目】如图,在四边形 ABCD 中,AD∥BC,E 为 CD 的中点,连接 AE、BE,延长 AE 交 BC 的 延长线于点 F.
(1)△DAE 和△CFE 全等吗?说明理由;
(2)若 AB=BC+AD,说明 BE⊥AF;
(3)在(2)的条件下,若 EF=6,CE=5,∠D=90°,你能否求出 E 到 AB 的距离?如果能 请直接写出结果.
相关试题

