【题目】观察图,回答下列问题:
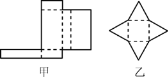
(1)甲、乙两图分别能折成什么几何体?简述它们的特征;
(2)设几何体的面数为F,顶点数为V,棱数为E,请计算(1)中两个几何体的F+V-E的值.
参考答案:
【答案】(1)见解析;(2)2.
【解析】(1)甲、乙两图能折成的几何体分别是长方体(四棱柱)与四棱锥.(2)长方体有6个面,8个顶点,12条棱.
解:(1)甲、乙两图能折成的几何体分别是长方体(四棱柱)与四棱锥.长方体由6个面围成,其中有2个大小相同的底面,侧面都是长方形且侧棱长相等,四棱锥由5个面围成,它只有1个底面,侧面都是三角形.
(2)长方体有6个面,8个顶点,12条棱,所以F+V-E=2;四棱锥有5个面,5个顶点,8条棱,所以F+V-E=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

-
科目: 来源: 题型:
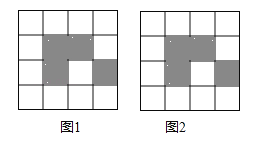
查看答案和解析>>【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它表示甲乙两人从同一个地点出发后的情况.根据图像判断,下列说法错误的是()

A. 甲是 8 点出发的
B. 乙是 9 点出发的,到 10 点时,他大约走了 10 千米
C. 到 10 点为止,乙的速度快
D. 两人在 12 点再次相遇
-
科目: 来源: 题型:
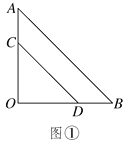
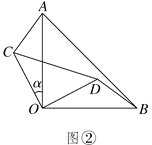
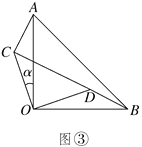
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
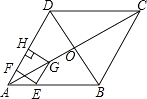
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为;当OO′⊥AD时,t的值为 .
相关试题

