【题目】如图![]() ,矩形
,矩形![]() 的两条边
的两条边![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
轴上,已知点![]() 、点
、点![]() .
.
(1)若把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,求折痕
,求折痕![]() 的长;
的长;
(2)在(1)的条件下,点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图![]() ,若
,若![]() 为
为![]() 边上的一动点,在
边上的一动点,在![]() 上取一点
上取一点![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 顺时针旋转一周,在旋转的过程中,
顺时针旋转一周,在旋转的过程中,![]() 的对应点为
的对应点为![]() ,请直接写出
,请直接写出![]() 的最大值和最小值.
的最大值和最小值.


参考答案:
【答案】(1)折痕![]() 的长为
的长为![]() ;(2)点
;(2)点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 的最小值为
的最小值为![]() ,
,![]() 的最大值为5.
的最大值为5.
【解析】
(1)连接AD,根据矩形的性质可求出![]() ,继而得
,继而得![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中,根据勾股定理求出DC长,继而在
中,根据勾股定理求出DC长,继而在![]() 中
中![]() 利用勾股定理求出DF长,证明
利用勾股定理求出DF长,证明![]() ,由全等三角形的性质得EF=DF,进而可求得答案;
,由全等三角形的性质得EF=DF,进而可求得答案;
(2)分两咱情形分别讨论即可:DE为菱形的边;DE为菱形的对角线;
(3)由题意点M在如图3中的圆环内或两个圆上,利用图象法即可解决问题.
(1)连接AD,

![]() 四边形
四边形![]() 是矩形,
是矩形,![]() ,
,
![]() ,
,
由折叠可得:![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,即
,即![]() ,
,
在![]() 中
中![]() , 即
, 即![]() ,
,
解得![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() ,
,
![]() ,
,
![]() ,
,
![]() 折痕
折痕![]() 的长为
的长为![]() ;
;
(2)由(1)可知,![]() ,
,
①当![]() 为菱形的边时,
为菱形的边时,![]() ,可得
,可得![]() ,
,
②当![]() 为菱形的对角线时,
为菱形的对角线时,![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,
重合,![]() ,
,
③当点![]() 在第三象限,
在第三象限,![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,![]() ,
,
综上所述,点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
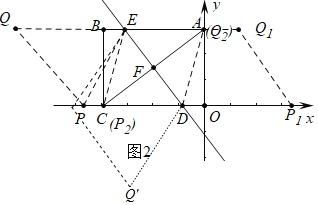
(3)如图![]() 中,作
中,作![]() 则
则![]() ,
,

观察图形可知,![]() 的最小值
的最小值![]()
![]() ,
,
![]() 的最大值
的最大值![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究

(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C=______;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案______.
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需要说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
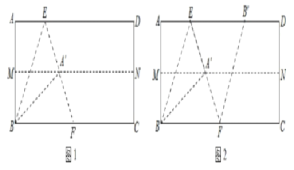
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
(1)证明:∠ABE=30°;
(2)证明:四边形BFB′E为菱形.
-
科目: 来源: 题型:
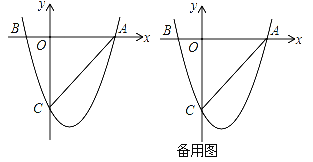
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=
 ,则AD=______ .
,则AD=______ .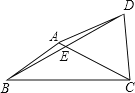
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )
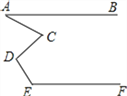
A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示
 梯形ABCD中,
梯形ABCD中,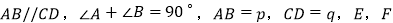 分别为
分别为 的中点,求EF.
的中点,求EF.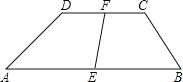
相关试题

